The Nature of Noise
Bruce Edmonds
Centre for Policy Modelling
Manchester Metropolitan University
http://bruce.edmonds.name
Introduction
The idea of noise plays a prominent (if subsiduary) part in many fields of study; it is casually mentioned in numerous papers as if its nature was well established. However to a large extent the term is not examined, but simply used. In other words, it has become part of the practice of science without entering to a significant[1] extent as part of its explicit theory[2].
The Oxford English Dictionary presents the following account (after a list of descriptions of more mundane uses referring to the older, non-technical uses of the word noise):
“11. a. In scientific and technical use: random or irregular fluctuations or disturbances which are not part of a signal (whether the result is audible or not), or which interfere with or obscure a signal; oscillations with a randomly fluctuating amplitude over a usually continuous range of frequencies. Also in extended use: distortions or additions which interfere with the transfer of information.…
b. In non-technical contexts: irrelevant or superfluous information or activity, esp. that which distracts from what is important.”
Thus we have a veritable “hairball” of related ideas, including: randomness; irregularity; disturbance; interference; obscuration; non part of a signal; distortion; addition; irrelevance; superfluity; and distraction applying to either a signal or to “what is important”. I think this accurately represents the term as it is used in technical papers (both in terms of content and in its vagueness). I this paper I try to produce a clearer and more coherent account of the term – an account that moves towards a more general theory of noise.
I start with a picture of noise from electrical engineering, since this seems to be where the concept arose first in academic papers[3] and so frames much of the scientific thinking on the subject. I then generalise this picture to the widest conception: that of noise as what is unwanted, which relates to our aural experience. A closely related conception that has developed in the scientific literitature is noise as what is unexplained – the residual after what can be explained (or modelled) is factored out. A particular case of this later usage is where a source of randomness can be used to stand-in for this residual. This strategy has lead some to almost identify hoise and randomness. However I argue that noise and randomness are not the same and thoughtlessly conflating them can result in misleading assumptions. I explore the possible relation between noise and context, and propose a new conception of noise, namely that noise is what can result from an extra-contextual signal. I claim that this is not only a pschologically plausible account of its origin (an hence relates well to common usage) but is also a useful way of conceputalising it. I finish with an application of the analysis of noise to the relation of determinism and randomness.
A picture of noise from electrical engineering
The close correspondance between electrical and acoustic phenomena allows the transfer of the term “noise” from an audible description to that which describes elements in the electrical phenomena that generates the sounds via a loud speaker. When you hear reproduced sound that is generated by electrical apparatus and compare it to the orginal sound, it has changed: a “hiss” has been added that sounds like (and acts like) noise. Thus noise becomes a technical term by analogy, however the way it was done is important and seems to have influenced the idea’s subsequent development.
The focus of much work in electrical engineering is the manipulation of identifiable electrical signals. These signals are the patterns or values encoded by the properties of a real electric current or field. To be precise, the signals are the intended patterns or values that are represented in actual (i.e. implemented or observed) flows of electrons and the forces between electrons. This distinction between electrical signal and eletrical phenomena is important because it marks the shift from a scientific point of view, where one is trying to discover the properties of the observed world, to an engineering perspective, where one is trying to manipulate parts of the world to obtain a desired effect. Of course, there is no well-defined boundries between these two approaches, and in practice many who work with electrical phenomena will, at different times and for different purposes, swap between scientific and engineering viewpoints. It is noticable that ‘noise’ enters the scientific literature only when we were able to control these effects sufficiently in order to be able to manipulate electrical phenomena in intended ways.
In electrical engineering you have a set of inputs and outputs that pass through a set of (usually well-defined) circuitary. The aim is to effect an intended transformation upon the inputs, which become the outputs. The transformations are implemented by (on-the-whole carefully manufactured) components such as transistors, diodes etc. The heat and nature of these devices means that the intended transformation is imperfect. For example an amplifier may be supposed to evenly increase the amplitude of a signal but otherwise leave it unchanged, but in reality will also distort it, add ‘hiss’ that is audible when broadcast etc. This situation is illustrated below in Figure 1.
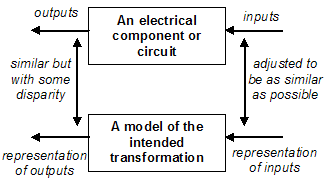
Figure 1. The disparity between the actual and ideal outputs of a circuit
In electrical engineering there are relatively good models for the action of such components (or conversely, we have learnt to manufacture components so that they are well represented by our models). Often these models not only specify the principal transformation effected by a component but also the give some information about the nature and extent of the imperfections, particularly the result of heat (and other entropy producing processes). This kind of understanding goes back to (Einstein 1905) and seems to pre-date the technical use of the word “noise”. Although the detail of this noise is unpredictable, it is particularly well characterised in terms of its general properties and is closely mimicked by a random statistical process – we call this ‘white’ noise. Thus many models of electrical components reify this as a distinct ‘noise term’, which may be otherwise undefined, or may with a defined probability distribution and related its magnitude to conditions such as temperature. The source of this particular kind of imperfection is relatively well understood, predictable and perceptable – it thus is natural to conceptually separate it out and label it as ‘noise’. Thus the notions of the intended signal and the actual phenomena diverge. I illustrate the result of this process of abstraction in Figure 2.
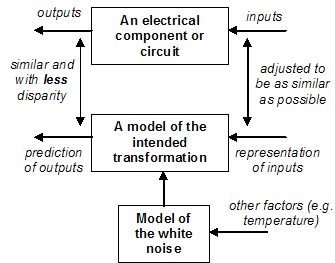
Figure 2. The smaller disparity when noise it reified and explicitly represented
This shows that it can be undoubtably useful to think of noise as a separate and indentifiable extraneous factor that is ‘added’ to the signal to obtain a more realistic prediction of the results. The combined model is composed of two submodels: the original and the model of the residual[4]. This coincides with the ‘shift’ from a scientific viewpoint of such circuits to an engineering viewpoint. As Wong (2003) puts it:
“Particularly, to the physicist the noise in an electronic system represents a practical manifesting of the phenomena described by statistical mechanics, and an understanding of its practical consequences helps to illuminate and clarify some concepts of the physical theory; to the electronics engineer, noise is a constraint of the real systems, but a better understanding of its physical origins helps the engineers to minimize its effects by informed and careful design.”
Within electrical engineering there is a continuing awareness that the randomness is just a model for the noise and that this model has its limitations. Pierce makes it clear that the noise is the primary descriptor and randomness part of the model when he says (1956):
“Many sorts of electrical signals are called noise … many engineers have come to regard any interfering signal of a more or less unpredictable nature as noise. … The theory of noise presented here is not valid for all signals or phenomena which the engineer may identify as noise.”
This practice is now quite common in many fields, often indicated by the appearance of a ‘noise’ term[5] in equations. However it should be remembered that this case is quite a special one. This particular kind of distortion particularly well-understood, predictable and seperable. It is also only one particular kind of distortion that can occur, albeit often a dominant one – other kinds such as resonance, interferrence, distortion etc. also occur and are more difficult to predict/model partly because they are less seperable from an intended (or significant[6]) pattern. Mimicking this step of using a single reified source called noise to stand for a general dissparity between explained and actual outcomes is likely to be much less useful in many other domains.
Some of what makes this a special case (i.e. justifies the attribution of ‘noise’ to error) is summarised as follows:
· The input signal and the intended results are known;
· There are good predictive model of the intended transformations involved;
· The whole system is engineered in a controlled way – the composition of the parts is explicitly known;
· The principal disparity between ideal and actual is well-understood;
· Many of the dissparity’s characteristics are predictively modelled as a separate part of the model;
· This dissparity can be characterised numerically so that the total dissparity for a system can be estimated mathematically;
· This disparity is easy to identify and even directly percieve.
These conditions have made the reification of noise as kinds of randomness a useful, if minor, field of study[7]. Analagous conditions are evidently not true for many other domains of study, and yet this idea of a seperable source of noise being mixed in with a significant signal has become a common one. In the next section I consider a generalisation of the concept of noise to include the wider cases.
Noise as unwanted interference
Noise can be seen as a largely a negative idea – as humans we are often interested in specific sound signals in terms of communication, music etc. and other sounds may make the task of identifying these signals more difficult. The difference between a set of measurements and an ideal is often attributed to ‘noise’ – in this case it is precisely what is not the ideal. This is the older use of the term, that precedes its entrance into the academic literature. If you are trying to listen to the radio and there are busses travelling outside or even people talking you may lump these together as 'noise', since they are extrenuous to what you were concentrating upon. One pair of people talking may be noise from the point of view of another pair of people talking and vice versa.
Noise here actually or potentially gets in the way of a perception or observation. A signal that has no chance at all of interferring with another is simply an irrelevant signal. Even if my neighbour's car generates a lot of sound inside its engine as a side effect of its operation, it is not noise if its silencer is such that this never escapes so as to disturb me. Thus a silencer on a car eliminates noise, even if the sound levels inside that engine remain the same. It is critical that if one counterfactually imagines the sound as escaping then it is natural to think of this as potential noise.
This conception of noise has, by analogy, now extended beyond aural noise – it is now commonly used as a generalisation of this idea. Thus an electric drill might be said to generate electrical ‘noise’ which might interfer with the reception of my TV. The essential aspects of this generalised conception seem to be that:
· there is an identifiable source of the ‘noise’
· that intefers with the reception of a target signal
· such that the noise is not intrinsic (or essential) to the signal and its transmission.
A non-electrical example of this kind of noise is interferences in gene expression (Blake et al. 2003).
Noise as unmodelled residual
To a modeller, noise is that which prevents one from modelling a process with complete accuracy. In a way the noise is something that is interferring with the modelling results, and so can be seen as analogous to the characterisation of noise in the previous section. Thus an econometric model may be composed of an indentified trend plus a noise term to 'account' for the deviations from this trend.
This is a presumptious use of the term – it implies that the 'noise' is something which may mask the hypothesised trend but is judged to be ultimately irrelevant to it. It thus suggests that the disparity is not simply due to modelling error, i.e. that there is not an accessible better model that would do better.
Nonetheless attributing modelling error to noise is sometimes appropriate – if you count the number of children at a children's party where children are not allowed to enter or leave and you get a different count each time then one can safely attribute the error to measurement “noise” (expressed in the chaotic movement of the children) rather than fundermental model error (the model being that there is a fixed integral number, n, of children in the room). You can senisibly model the sequence of counts as a fixed constant plus a noise term (which might usefully be given a random nature).
Whatever the purpose of the modelling, a discrepancy between the model outputs and target data gained from measurement of the modelling target is an indication that there is something in the target+measurement processes that is not captured by the model. In other words, the data itself is another model, a “data model” (Suppes 1962). If one has some good reasons to attribute this discrepancy to some factors that are not relevant to (in the sense of “arbitrary with respect to”) the model and its purpose, then it can be properly called noise.
When modelling complex phenomena (e.g. social phenomena) it is inevitable that one is not going to be able to capture all aspects of ones target in any single model and hence one would expect that there will be a dissparity between a model's outputs and the corresponding data obtained from the target. The key question is whether this discrepancy is due factors that are relevant to the modelling task or orginate from a process that is independent and irrelevant.
Conflating noise and fundermental model error can be very unhelpful. I will illustrate this with an example from the insurance industry.
Example 1: The estimation of insurance claims
This case concerns the estimation of the frequency of events in the insurance industry. Before 1990, the distribution of insurance claims was thought to be roughly normal, that is when one plotted a the frequencies of periods with different levels of claims the result fitted a normal curve well except for a few periods with a very high level of claims However these few cases were discounted as due to particular circumstances and hence unmodellable. This model of a normal distribution plus some arbitrary events was used to set premiums. However more recently a series of models which explicitly includes and predicts such “extreme” events have been re-discovered and applied (Black 1986, Andersen and Sornette 2001).
Example 2: The ‘noise traders’
There is a model of stock markets which has two types of trader (Delong et all 1990): those that invest according to the ‘fundermentals’ of stocks and ‘noise’ traders who speculate randomly. Their combined actions serve as a candidate explanation for the sort of movements observed in stock market indicies. The individuals in the model that stand for these traders can swap between these two types, so a trader that was formerly a fundermental trader may become a noise trader and vice versa. The noise traders essentially act randomly, but the swapping between the behavioural types is as a result of the prevailing stock market conditions and the thresholds of that particular trader.
Many social models attempt to use statistical models to seperate out social trends from the 'noise', under the assumption that human actions can be represented en masse as trends plus arbitrary actions that tend to cancel each other out (in large samples). If that ‘noise’ is supposed to be effectively random, then this is a hypothesis that can be tested, since in increasingly large samples the noise will not grow as fast as the signal and will thus fall as a proportion of the population size (something that is not obviously true of stock markets). This is called the “law of large numbers”. This may be justified as in (Dichev 2001) but in other cases it is not, as demonstrated by the models of (Kaneko 1994, Edmonds 1999a).
Indeed we are so used to the idea of seperating out a signal from added random noise that we forget what a special case this is, as (Van Kempen 2001) put it:
The amazing thing therefore is not that they [fluctuctuations] give rise to irregular phenomena. The amazing thing is that a collective behavior emerges, which is regular and can be described by general law...
Noise and randomness
In the special case where we are trying to model a particular data-generating process, we may well get to the stage where we have included in the model any systematic pattern we can detect in the data. In such a case what is left is precisely what we can not systematically model, namely a residue that is effectively upredictable[8]. This residue is, by construction, not modelled. However it might be possible to adjust the model so that the secondary characteristics of this residue are modellable. For example, although each point is unpredictable, the statistical moments of an increasingly large sample of this data may converge to particular values. These values can be used to construct a sort of model of these residuals – a statistical model. Such a statistical model is composed of a particular probability distribution, from which values can be randomly (or pseudo-randomly) generated. This random series of values is not the same as the unmodelled residual but 'looks' the same to us as modellers – each has the same known distribution and the same unpredictable content within this. If we deem that the unpredictable residue is not relevant then we can say that in all relevant aspects the random series and the residue are the same. Thus it is that we often think of this unmodelable residue as random – they look the same to us and (by construction) from the point of view of the model their detail is equally irrelevant[9].
Such a perspective might lead one to conflate such noise and randomness and identify noise as randomness. However, this is simply to confuse a model (randomness) with what is modelled (noise). That they are not necessarily the same as the following examples show.
Example 3: The interspersed coded-messages
Imagine two different messages (strings a and b) that are both encrypted (to strings x and y) by different people (A and B respectively) so that each appears to be a random sequence to anyone but the person who encoded it. Then the two sequences are interspersed to form a single sequence (c). To A the part of c that is y is just noise, there is nothing modellable about y, only x has meaning. To B the part of c that is x is the noise whilst the y part has meaning.
The part that is noise for one person is the signal for the other and vice versa. Thus either randomness is a relative concept or it is different from noise (which in this case is clearly relative).
One might think that such a type of sequence would not result from any natural process, but this is only an assumption. If it is possible to make an unguessable binary sequence, then it is possible to implement such a data-generating process as a program on a computer. Thus if we had such a computer attached to a Giger counter and a small lump of radioactive material (to generate the random input), and we always plug more memory into it as required, we could produce such a sequence. Thus although highly contrived such an example is not beyond the bounds of possibility for a natural process.
Example 4: The sabotaged random number generator
Imagine a company that sells good quality random sequences, that is sequences with well-defined long-term statistical properties but with no guessable patterns in the detail at all[10]. Say that they did produce sequences which passed all the requisite tests for randomness. Now say that an agent for a rival company interferred with the set-up by adding an extraneous signal to the process which caused the product to now fail some of the tougher tests for randomness.
That agent evidently introduced some noise into the system, but it was not purely random because it decreased the randomness of the result. Here randomness and noise are not the same but are opposed.
What is the case is that sometimes (as in the electrical engineering case above) it is useful to think of this unmodelled residual as arbitrary (particularly if one has good reason to believe that it is irrelevant to the modelling task in hand) and can be usefully represented by a random distribution. This is a natural thing to do since randomness is a positive way to think about noise which otherwise is a negative (what we don't want/understand/represent). In many modelling techniques (e.g. many simulations), it is useful to use a random source to ‘stand-in’ for parts of the model thought to introduce this arbitrariness. Then one can use techniques such as ‘Monte Carlo Sampling’ to try and separate out the effects of these parts from the tendancies exhibited by the rest of the model.
However arbitrariness and randomness are not the same as one can not guarantee that an arbitrary signal will not suddenly exhibit some pattern, which may turn out to be significant. This is shown clearly in the example of the ‘Millenium Bridge’ in London.
Example 5: The Millenium Bridge
The Millenium Bridge is a beautifully elegant structure that spans the river Thames from the bank below St. Pauls to the Tate Modern gallery. This was carefully designed and the design was extensively simulated before being built. However, a few weeks after it was opened it had to be closed again for dampeners to be fitted, as it was prone to oscillations that were deemed a danger to the public. It seems that what happened is that in the simulations of the design the movements of people were assumed to be random, but with large numbers of people they reacted to small movements in the bridge so as to amplify the movement. The small oscillations had the effect of synchronising peoples’ reactions and hence having a much greater effect. The result was that the unmodelled reactions of individuals and their coupling via small swayings of the bridge were far from random. Indeed, if they had not happened to cause this particular effect they could have safely regarded as arbitrary and hence modelled using a random ‘stand-in’, however that did not turn out to be the case (ARUP 2001, BBC News 2000).
Noise and context
Let us look back at the picture of noise that we started with, that of electrical noise originating in electronic cicuits. In one sense this is a very odd usage – noise here does not come from an arbitary source but is part of the intrinsic nature of the electrical components. From a more objective point of view it is amazing that it is possible to construct ensembles of components that act so as to effect the desired transformations with such an astounding degree of accuracy. It would be less strange if such an ensemble only produced white noise whatever its input than it transforms the inputs to the desired outputs with such accuracy. It is only due to the huge scientific and engineering effort that has lead to a situation where we can expext such perfection and hence reify any shortcomings as a seperate entity called 'noise'.
Similar shifts occur in other situations; if one is trying to listen to person A talking then person B talking may be noise, and vice versa. What is noise depends on who one is trying to listen to.
A possible explanation for this is the context-dependency of modelling. Any model of observed phenomena has a set of conditions under which it is effectively applicable. Not all of these are explicitly included in models but rather the kind of context where a model is applicable is recognisable. The context ensures that, on the whole, these implicit conditions hold and that the model can be represented in a relatively simple and manageable form. The fuzziness of the context recognition allows the model content to be relatively well-defined and 'crisp'. This crispness allows us to reason about the content of such models. This necessary context-dependency in modelling is quite a separate matter from whether the model is generally applicable in theory. For example, the laws of Newtonian physics presumably hold to an astounding degree of accuracy (in circumstances where relativistic and quantum effects are negligible), but may not be practically applicable in a situtaion where well-defined objects are difficult to identify.
The context-dependency of learning and application of knowledge and models makes these processes much more feasible. However, this 'trick' only works when the conditions under which a model is learnt are effectively recognisable, so that one knows when one can reliablely apply a model. For more on the pragmatic roots of context see (Edmonds 1999b).
Error in a model's output's compared with observations could be due to several things: it could be due to sheer model error within the context; the context itself could have been wrongly identified; or the error could originate from without the assumed context. A coherent picture of noise comes about when the source originates from outside the assumed context – we do not want to reject the model (this still works at some level), and the assumed context seems to be the appropriate one (many other models associated with this context are working well) so the source of the error must lie elsewhere.
This picture of an extra-contextual cause of model error accounts for all the properties of noise we have identified above. In turn it accounts for:
· The arbitrariness of noise, since it comes from outside the context (since a modelling context is supposed to contain everything pertinent);
· The dependency of the identification of noise on context – thus in the “Two person's talking” example for each person the context focused on excluded the other talking;
· That the noise has to be able to interfer in the foreground model, since otherwise it has not entered the context as in the “Car Engine” example it depended on whether we imagined the sound escaping into our context (unless we imagined it doing so);
· That the shift from detecting the random fluctuations in the potential difference accross a piece of conducting material at thermal equilibrium to the attempt to reduce interference with an audio signal in an amplifier corresponds to the reification of noise.
Noise and the “excluded middle” between randomness and determinism
The thesis of determinism is widely held. To a thorough determinist any randomness is merely a result of incomplete modelling. In other words, all apparent randomness is only an unmodelled residue[11] – in principle it could all be modelled. Quantum mechanics forces many to accept that there is also unreducible randomness in the universe[12]. Thus the assumption of many is that, in principal everything can be satisfactorily modelled as deterministic processes, except for a random residual – that is the world is neatly divided between the deterministic and the purely random. Certainly there are many that assert that almost all macroscopic events and processes are essentially deterministic[13], in the sense that all relevant parts of the process can be satisfactorily represented as a deterministic process and the rest is not significant and so representable by random noise.
This picture coincides with the common modelling practice of using a pseudo-random source as a stand-in for an unmodelled residual, thus in the “noise traders” example above the unexplained “irrational” behaviour was modelled as random behaviour. This can be an appropriate approach is there is good reason to suppose that the residual is arbitrary to the modelled process so that the pattern of this residual does not make any significant difference to the model outcomes (which depends on the model use). A conflation of this modelling approach and a deterministic bias seems to lead some to the conviction that any unmodellable residual (a residual that is not capturable in a model in theory) must be random.
A particular case of such a conviction is that anything that is not deterministic must be random. That is the view that the world is divided between the random and the determined. In this view it may be that some things that appear random turn out to be merely very complex (i.e. we find a way to explicitly model the phenomena where we previously used a random/statistical proxy), and it may be that some things that appear deterministic are so only because of some grand “averaging out” of randomness at the detailed level (such as the atoms in a gas), but ultimately that is all there is: deterministic processes and random ones.
Such a view is closely related to the view that there are no essentially correct models that are necessarily context-dependent. That is to say, that is it always possible to reformuate a model to arbitrarily widen its scope – so that an essentially context-free model is possible. Given such an assumption it is always possible to claim that any unmodelled residual can be eliminated by expanding the model. A slightly weaker form of this assumption is that any non-random unmodelled residual is thus eliminable.
However if, on the other hand, some models are intrinsically context-dependent then this is far from necessary, the residual might not be modellable from within any appropriate context and the model might not be possible from within other (e.g. wider) contexts. Another way of putting this is that even the most appropriate context is not hermetically sealed, for there is inevitablly some 'interference' from without. In this case the ‘interference’ might not be modellable but there is no reason to suppose that it is best ‘represented’ as a random term either[14].
In many mundane cases it is clear that ‘noise’ does not have to be random. The noise of a bus in the street that is interferring with listening to a radio programme is not random just as the “ringing” of transistors after they have switched is not random. Neither are many chaotic systems random, as one can tell by an inspection of their mechanism, even if it is difficult to distinguish their ourcomes from random outcomes[15]. As (Boffetta et al 2002) puts it:
…the distinction between chaos and noise … makes sense only in very peculiar cases, e.g., very low-dimensional systems
One response of those who model electrical circuits to the inadequacy of modelling all electrical noise as “white noise” (that is noise which includes, at random, all frequencies) is to enrich the modelling of noise with properties other than the pure form of regulated randomness that characterises “white noise”. As Ritter (2003) put it:
Both are fundamental sources of "white" noise, meaning that we have a deep statistical understanding of how these sources behave. Unfortunately, this may not be particularly useful if the noise we have is actually due to variable processing-related problems.
Thus a variety of kinds of noise have now been developed, including “grey” and “black”. If it is right that noise is inherently context-dependent and not necessarily random then there will be no “new” kind of proxy for noise that will always be applicable. Determining what might be the most appropriate proxy for an unmodelled residual is an extremely difficult problem, one where it is difficult, in principle, to know what is most appropriate because this would require knowing something about modelling the unmodelled residual, which is not easily ameanable to explicit modelling.
Conclusion
Noise, in its more general usuage can be usefully though of as extra-contextual inteferance in what is being modelled. All effective modelling is context-dependent, and no context is completely “water tight” to influences from outside the context, influences that due to the nature of context are unmodellalbe. It is these influences that may interfer with the accuracy (and, indeeed, applicability) of our model – we call these influences “noise”. We often model these influences with a random “proxy” because randomness is also unmodellable (in the sense of point-by-point detail).
Athough many take randomness to be an essential property of noise, it should be clear from the analysis above that noise is not necessarily random but can be merely arbitrary with respect to the target. The confusion comes about because we use often randomness as an architypal model for noise. Noise may be of almost any nature considered in isolation – it is only the poverty of our imagination that insists on casting it as its architype.
References
Anderson, P.W. (1997) Some Thoughts About Distribution in Economics. In W. B. Arthur, S. N. Durlaf and D.A. Lane, (eds.) The Economy as an Evolving Complex System II. Reading, MA: Addison-Wesley, 566. ***
Andersen, J. V. and Sornette, D. (2001) Have Your Cake and Eat It, Too: Increasing Returns While Lowering Large Risks! Journal of Risk Finance. 2(3):70-82.
ARUP (2001) The Millenium Bridge. ARUP’s (the engineer’s) site on the Millenium Bridge. http://www.arup.com/millenniumbridge/ (accessed 15th May 2003).
BBC News (2000) The Millenium Bridge. A BBC News report on the Millenium Bridge. http://news.bbc.co.uk/hi/english/static/in_depth/uk/2000/millennium_bridge/ (accessed 15th May 2003).
Black, F. (1986) Noise. Journal of Finance, 41:529-43.
Blake, W. J., Kaern, M., Cantor, C. R., Collins, J. J. (2003) Noise in eukaryotic gene expression. Nature, 422(6932):633-637.
Boffetta, G., Cencini, M., Falcioni, M. and Vulpiani, A. (2002) Predictability: a way to characterize complexity. Physics Reports 356(6):367-474.
Cartwright, N. (1983) How the Laws of Physics Lie. Oxford: Oxford Univerity Press.
Compagner, A. (1991). Definitions of Randomness. American Journal of Physics. 59(8): 700-705. ***
Delong, J. B., Shleifer, A., Summers, L., and Waldmann, R. J. (1990) Noise trader risk in financial markets, Journal of Political Economy 98, 703-738.
Dichev, I. (2001) News or noise? Estimating the noise in the US News university rankings, Research In Higher Education, 42(3):237-266.
Edmonds, B. (1999a) Modelling Bounded Rationality In Agent-Based Simulations using the Evolution of Mental Models.In Brenner, T. (ed.), Compuational Techniques for Modelling Learning in Economics, Kluwer, 305-332.
Edmonds, B. (1999b) The Pragmatic Roots of Context. CONTEXT'99, Trento, Italy, September 1999. Lecture Notes in Artificial Intelligence, 1688:119-132.
Einstein, A. (1905) Investigations on the Theory of Brownian Movement. Annalen der Physik 17:549-; (A.D. Cowper transl.), Methuen, London (1926) and Dover, New York (1956).
Gupta, M. (Ed.) (1977) Electrical Noise: Fundamentals and Sources. IEEE Press. 51-58.
Habermas, J. (1963) Theorie und Praxis. [Frankfurt am Main] : Suhrkamp Verlag. (English trans. Viertal, J. (1988) Theory and practice. Polity Press).
Hesse, M. B. (1963). Models and Analogies in Science. London, Sheed and Ward.
Hughes, R. G. (1997) Models and Representation. Philosophy of Science, 64(proc), S325-S336. ***
Kaneko, K. (1990). Globally Coupled Chaos Violates the Law of Large Numbers but not the Central Limit Theorem. Physics Review Letters, 65: 1391-1394.
Kolmogorov, A. (1965) Three Approaches to the Quantitative Definition of Information. Problems of Information Transmission. 1:1-17. ***
L'Ecuyer, P. (1992) Testing Random Number Generators. Proceedings of the 1992 Winter Simulation Conference. 305-313.
Morariu, V. V., Coza, A., Chis, M. A. , Isvoran, A., Morariu, L. C. (2001) Scaling in cognition. Fractals-Complex Geometry Patterns And Scaling In Nature And Society, 9(4):379-391. ***
Peterson, I. (1997). Lava lamp randomness. Science News 152(Aug. 9):92. http://www.sciencenews.org/20010512/mathtrek.asp
Pierce, J. (1956). Physical Sources of Noise. Proc. IRE. 44:601-608. Reprinted in (Gupta 1977), 51-58.
Ritter, T. (2003) Random Electrical Noise: A Literature Survey. http://www.ciphersbyritter.com/RES/NOISE.HTM (accessed 15th May 2003).
Suppes, P. (1962) Models of Data. In Nagel, E; Suppes, P; Tarski, A (eds.). Logic Methodology and the Philosophy of Science: Proceedings of the 1960 International Congress. Stanford, CA: Stanford University Press, 252-261.
van Kampen, N.G. (2001) Foreword: The Theory Of Noise. Fluctuation and Noise Letters, 1(1):3-7.
Wong H. (2003) Low-frequency noise study in electron devices: review and update. Microelectronics Reliability, 43(4):585-599.