[Next] [Previous] [Top] [Contents]
Towards a Descriptive Model of Agent Strategy Search - Bruce Edmonds
The experiment is divided into parts: 0, 1, 2, 3, and 4, each of 4, 15, 15, 15 and 20 games respectively. Part 0 is the practice stage where the agent learns but statistics are not kept and no earnings gained. In parts 1, 2 and 3 the agents learn and earn as they do so. In part 1 the game starts in earnest, so that the subjects earn real money dependent upon their performance. At any stage in the game the subjects have the option of finding out any combination of the following information about the game so far: the number of bids; the last bid; the highest bid so far; the cost of bids if they stopped; and the earnings if they stopped. Part 2 is the same as part 1, except that at any stage the subjects can only access one of the above pieces of information (this does not stop them remembering or working out this information in their head, of course). In part 3 the first 0, 1, 2, 3 or 4 offers (determined randomly) were automatically accepted, the subject deciding when to stop after that (these offers still had to be paid for). In the last part (part 4) a constant strategy (the best learnt by the end of part 3) is kept for each game, so no learning occurs but statistics are kept and payments made.
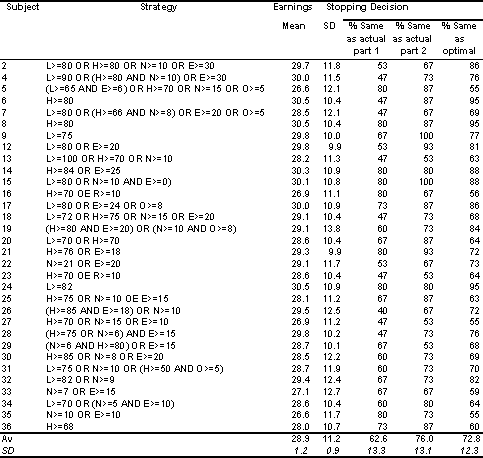
What makes this particular experiment appropriate for this purpose is that Sonnemans extracts the strategies that the subjects end up with in a form that is computationally modellable. In the experiment there were several parts. In the initial parts the subjects were able to try out their strategies. Before the last part they had to specify the strategy that would determine offer acceptance for the final 20 games. In all but two cases these could be formulated in terms of five predicates and two Boolean operators. This is not surprising as Sonnemans had done a pilot study to determine the operators that most people would use. These were: Hxb3 x (the highest offer so far is not less than x); Lxb3 x (the last offer was not less than x); Nxb3 x (there have been x offers or greater); Exb3 x (earnings are not less than x); Oxb3 x (there have been at least x offers in a row since the last highest offer or more); AND (boolean conjunction); and OR (boolean disjunction). Thus the strategy `Accept the highest offer if my earnings are at least 70 or there have been 10 offers' could be expressed as `Hxb3 70 OR Nxb3 10'.
Two of the strategies were of a form which would entail a non-zero probability of never terminating (e.g. only stop if earnings are greater than 90). Two of the strategies were of the form stop if the earnings are at least X(t), where X is a function and t is the earnings so far. These four strategies were excluded from the results reported by Sonnemans*1. The other 34 strategies are shown in Table 1.

Table 1: Derived from Table 3 of [12], page 317. The strategies of the subjects in part 4. The characters in the second column have the meanings as describe above. The earnings statistics and the percentage same as optimal are based upon a simulation, N=160 000.
As has been remarked in other experimental studies (e.g. [4, 6, 11]): subjects learn better strategies as they gain experience; overall efficiency is reasonably high, and there is a marked tendency to stop too early. This last fact is shown by the stopping statistics for the experiment shown in Table 2.

Table 2: Derived from Table 1 of [12], page 316. Search behaviour, 36 subjects, 15 periods per part. The earnings are in cent per period.
As Sonnemans points out, this early stopping behaviour is not explained by simple risk aversion in many cases. Figure 1 shows a plot of the mean earnings against the spread of earnings for the 34 strategies listed in Table 1. The line shows the orbit of optimal strategies for various risk/expected earnings trade-offs. Many of the strategies chosen by the subjects were under the top part of the line, so that there were other strategies they could have adopted with the same level of risk but greater average earnings.
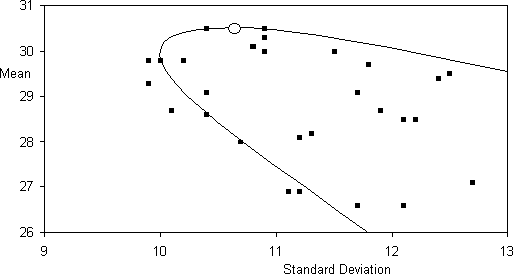
Figure 1: Derived from Fig. 1 of [12], page 319. The curve is the expected mean and standard deviation of the earnings of the strategies of the `optimal' form (i.e. those of form `Hxb3 x') and the black squares are the strategies that the subjects specified for part 4 (see Table 1). The expected performance by the risk-neutral `optimal' strategy (i.e. Hxb3 81) is indicated by the O (SD=10.6, Mean=30.5).
[Next] [Previous] [Top] [Contents]
Generated with CERN WebMaker