Towards an Ideal Social Simulation Language
Bruce Edmonds and Steve Wallis
Centre for
Policy Modelling
The Manchester Metropolitan University
http://cfpm.org/
1. Introduction
In this paper we discuss the purpose, design and direction of systems for the computational simulation of social phenomena. We do this by arguing and speculating about what an ideal system of this type might look like. We illustrate this with the tentative steps that have been made in this direction with respect to SDML. We hope that this will inform and stimulate the further development of social tools.
The ultimate aim of a social simulation is, trivially, to help us understand social phenomena. What is far from trivial is knowing what sort of understanding it can give us and how this may occur. A deeper insight into these issues may help us to design appropriate tools. A good social simulation tool will fit well with a good methodology, and an appropriate methodology will depend on the sort of knowledge we are after.
For this reason we will start with an examination of the process of modelling and from this list some of the general characteristics one might expect of an ideal social simulation language (ISSL). We will then describe some tentative steps towards reaching this ideal in terms of features implemented into the SDML modelling environment. Finally we will look forward to some of the possible advances that may take us further towards the ideal. The discussion will be illustrated in terms of the Schelling model, so if this is unfamiliar to you we suggest you first read the details of this archetypal social simulation in the appendix.
2. Modelling Social Systems
Modelling social systems is difficult. It is difficult for (at least) two reasons. Firstly, the complex interactions that are involved in social systems mean that the outcomes are difficult to analyse using traditional formal approaches — we will call this the ‘syntactical complexity’. One way of thinking about this is that the computational ‘distance’ from the system’s initial set-up to the outcomes is so great that is completely impractical (and probably unhelpful) to attempt to derive general properties of the outcome from the set-up in an analytic fashion. Secondly, the characteristics of social phenomena are frequently best approached using semantically rich representations (purpose, emotions, social pressure etc.) and these are difficult to translate into formal models — we will call this the ‘semantic complexity’. We will not discuss here whether there is a fundamental difference between these, since we do not want to get bogged down in the reductionist/holist debate. We will merely note that, given our present knowledge, there are at least significant practical differences (see Edmonds, 1996 for more on the pragmatic approach to reductionist/holist question, and Edmonds, 1999 on definitions of complexity).
The presence of syntactic complexity means that there will be at least two different views of a simulation: the interactive processes that are used to specify the simulation; and an appropriate representation of the significant outcomes. The syntactic complexity of the process detail means that it will not be easy to infer the later from the former. It is the presence of this complexity that necessitates the duality in our representations of the simulation: one for the design and one for the outcomes.
For example, in the Schelling model: firstly there are the detailed rules for the movement of black and white pieces – depending on a critical parameter specifying the minimum acceptable proportion of like coloured pieces in each piece’s locality in order to stay put – and secondly there is an ‘overview’ concerning the overall pattern – the extent to which the colours have ‘clumped’ together. The former might be expressed as the operation of a cellular automaton and the latter as some sort of statistical measure. The simulation is interesting precisely because it is difficult to see or prove why this clumping occurs from within the computational view for low values of the critical parameter.
If the outcomes are not easily deducible from within the ‘output’ view either, then we call these outcomes ‘emergent’. Many social phenomena fall into this category. In the Schelling model the ‘clumping’ outcome is not emergent for high values of the critical parameter, since it is fairly obvious from within the overview why the clumping occurs. However it is emergent for low values where the clumping occurs only because of detailed probabilistic dynamics at the edge of clumps.
The existence of semantic complexity means that modellers have three choices:
· they can concentrate on those parts of social systems that they think are effectively reducible to a syntactic representation;
· they can adopt a pseudo-semantic approach, where the simulation manipulates tokens which are undefined inside the simulation (where they are computationally manipulated) but which are meaningful to the humans involved (as found in both the set-up and outcome);
· they can avoid computational simulation altogether and stick to natural language (or the like).
The Schelling model only qualifies as social science because the mechanisms and results can be interpreted into the semantically rich domain of racial and cultural relations. Thus for the Schelling model (and many other social simulations) there are at least three relevant views: the computational view; the ‘overview’ (usually concerned with the outcomes); and the simulation’s intended interpretation in terms of observed social phenomena.
Of course, frequently there are more than just three relevant views. For example, there might be entirely different views and bases for different parts of a simulation — the cognition of the agents might be viewed in the light of a particular model from cognitive science, the computational mechanisms might be expressed as logic-like rules, the resulting population dynamics might be viewed using the analogy of a market, the communication between agents modelled as a process of mutual convergence and the whole thing interpreted as a representation of a population of web-based information agents. In fact unitary models are the exception in science — it is far more usual to encounter composite models of any but the most basic phenomena (Giere 1988, Cartwright 1983).
Another complication comes from the fact that, typically, models will take a lot of their structure from previous models and have outcomes that are validated against yet other models. This 'chaining' of models is inevitable when modelling complex systems. However, it does not discharge the onus to verify its structure or validate its outcomes, this is merely achieved via other models — thus such a model will only become finally acceptable if the whole chain is verified and validated. The chaining of models delays judgement on a model by making its verification and/or validation indirect, but it does not eradicate the need for such checking.
It is frequently the case that in social simulation that what is interesting is not so much the resulting states, but the processes that emerge from the simulation in terms of the overview. This is because the highly dynamic nature of many social systems does not allow us even the pretence of ceteris parabis prediction of representative states (as in economics), but rather we often use simulations to inform our semantic understanding of existing social processes. In the case of the Schelling model, most social scientists would not presume that they could actually predict the probability of self-organised segregation based on measurements of the critical parameter in real populations, but rather it informs their perception of the likelihood of the emergence of segregation among relatively tolerant populations, which they will then use as a part of their general evaluation of situations, along with the rest of their knowledge.
Thus the processes of interpreting the social phenomena into the code of a simulation and interpreting the outcomes back out again are, at least, as important as the internal workings of the simulation. For without good interpretation a simulation is just another computation[1]. The process of representing the social phenomena into a simulation is frequently associated with verification and relating the outcomes back again with validation.
Verification and validation are terms that come from software engineering. Verification is the process whereby one checks that a piece of software meets its specification and validation is where one evaluates the performance of the software against its goals. Simulation specifications are frequently missing from descriptions of social simulations. This is a pity as a specification would help separate out the implementation from the simulator's process of abstraction – it would form an intermediate level description of the author’s intention for the simulation. This would make the checking and critique of simulations easier (which is perhaps part of the reason why it does not occur too often).
We shall call the interpretation into a simulation the ‘representation’ of a social system and the interpretation of the outcomes back out as the ‘expression’ of the simulation. Using these terms, verification is the process of checking that the representation is faithful to the simulator's intentions and validation is the process of checking that the expression of the simulation is faithful to the relevant social phenomena.
Both representation and expression provide constraints on acceptable social simulations. The former acts to constrain the design of the simulation before it is run, while the later acts as a post-hoc check on its acceptability. They are thus both ways of constraining the simulation so that it strongly relates to the object social phenomena. From a scientific point of view we want our simulations to be as faithfully constrained as possible by the object social phenomena (or process).
Now, of course, things are not quite as simple as the above account of
representation and expression might suggest. Not only will our processes of
interpretation be biased by the available technology and our world view, but
sometimes the social phenomena will be intimately bound up with our perceptions
of it — in other words some real social phenomena are constructed by us. In
this case the constraint comes from society, but not in the guise of an object
of our interpretation but as an inescapable result of our perceptual and social
processes.
Also it is almost always the case in social simulation, that the object of study (or phenomena) is not directly modelled, but rather it is an abstraction of the original object that is modelled. The simulation provides understanding of the workings of the abstraction. This intermediate abstraction is frequently left implicit and sometimes it appears that some authors have completely conflated their abstraction with the object of study. Even when such an abstraction is legitimately and carefully introduced, it inevitably introduces a bias into the modelling process - the form of the abstraction will be inevitably biased by abstraction’s framework (Edmonds 2000). This is acceptable when: (1) the framework is chosen to suit (i.e. not unnecessarily distort) the original object of study w.r.t. to the goals of the modelling endeavour; and (2) the framework and its biases are acknowledged and documented.
In all cases enough constraints will have to be accumulated if the simulation is to be computationally well defined, i.e. so that a computer can execute it. The important question is where these constraints will come from. Some possible sources for these constraints are:
· From the object phenomena under study (either directly or indirectly);
· From previously well-validated models (or chains of models);
· From the processes of interpretation;
· From practical difficulties in implementing the intended specification;
· From theoretical a priori restrictions;
· From considerations of simplicity — i.e. general resource considerations;
· Other, essentially arbitrary, sources (e.g. programming error).
These types of constraints are to different degrees desirable and to different degrees avoidable (depending on the situation). Clearly, progress in the methodology of social simulation should aim to, in general, increase desirable constraints, decrease undesirable constraints, clearly separate the different types of constraint and document them all.
A methodology which distinguishes, documents and checks constraints (whatever their origin) deflates the constructivist/realist divide. A model that is categorised as realist is merely one which happens to be more highly constrained by the object under study — such a model reflects the object of study in those aspects in which it is constrained and to the extent that it is so constrained[2]. Where the model happens to be more weakly constrained by the target phenomena (the usual case in social simulation), so that an wider range of possibilities exist, then the biasing effect of the language of modelling and the focusing effect of our perceptions will be greatest — such a model is necessarily constructed in some ways, and if it is to have a social use these ways will have to be based on social commonalities.
In the former case the interpretation processes are closely specified by strong constraints which means that the syntactic content of the simulation becomes more important. In the latter there is more latitude for varying interpretations – where the construction of meaningful and useful functions of language are essential – so the focus tends to shift more towards the token processing aspect. Although the former case would seem to provide us with more certain knowledge in some sense, it is far from certain that it will be more effective in helping us understand social systems. There are several reasons for this: firstly, our semantic understanding of society is far more powerful and effective than our more formal theorising (at least currently); secondly, it is extremely difficult to obtain useful and reflective models of social phenomena; and finally, the aim of social simulation is frequently not to predict detail but to inform our semantic understanding anyway.
In practice, we will often not be able to tell whether the extent to which our models are constrained by the object social phenomena and how much by the social/linguistic constructive processes (in some cases it not even clear that such a distinction even exists). For example, there may not be any objective viewpoint from which to make such an evaluation. Nevertheless, regardless of this uncertainty, a methodology which attempts to distinguish, document and check the constraints that specify a simulation is helpful. It is helpful because a process whereby we can continue to criticise, specialise, generalise and systematically adapt simulations using explicit knowledge about the source constraints would allow a more rapid and effect simulation evolution. If we are intending to reduce a set of social phenomena to a syntactic simulation (so that the resulting model is relatable to other such models using formal methods) such models can be combined, compared and subsumed using well tried methods. In such a case well-documented constraints can considerably aid this process both in terms of guiding the formal processes and by providing the essential building blocks for the formal representation itself. However, if we are adopting a more pseudo-semantic token-manipulation approachable, being able to distinguish and document the processes and constraints we used to construct the simulation (including our intended interpretation of it) would ease the task of re-evaluating it from within different paradigms. This would increase the chance that parts of the simulation may be separated out and reused. Thus, even if future researchers have a very different view to us as to the sort of constraints that might be appropriate or even as to the correct attribution of constraints, if they are documented the research may still be valuable to them, because they will have the necessary information with which to reinterpret the work.
The sort of constraints we use can also be strongly related to our purposes in building and using simulations. A simulation at the more theoretical end, may only be weakly constrained by observation of social systems because its purpose is to try and map out some of the possible processes that could occur in such systems – it is a sort of ‘stand-in’ for an effective method of deductive inference from set-up to outcomes. This might be necessary due to the presence of syntactic complexity. Such a model needs to exhibit quite relevant, general and strong patterns of behaviour because its interpretation back into our semantic understanding is necessarily weak – the justification for doing this sort of simulation is that its results will be relevant to many other simulations[3]. A simulation at the more applied end will attempt to take the maximum possible constraint from the system under study both in terms of the set-up of the model as well as in terms of the results – the justification for doing this sort of simulation is sufficiently constrained by the object phenomena that insights gained from outcomes of the simulation are also applicable to the phenomena themselves. If these are weak then we can have little confidence that the simulation results are relevant at all to the target social phenomena.
3. Consequences for a Computational system for Social Simulation
Given the analysis above, what would we desire of a computational system for social simulation? Based on the analysis above we will extract some criteria for an ISSL. These will be far from exhaustive for we are attempting to be as generally relevant as possible.
1. The
system should be as free as possible of any particular social or cognitive
theory. Whatever theory exists to structure the system should be as clear as
possible so that its contribution can be cleanly distinguished from the
intended content.
This is, of course, true only of an ISSL that is intended to be generally useful. If a system is intended to embody a particular theory, and this theory is clear, then simulators who want to use or who accept that theory can work within this. Even then it is important that the structure that the base system provides is as well understood as possible, so that its influence of the process of implementation may be verified and documented. The importance of the intended theory/implementation separation was raised in (Cooper et al. 1997) where they show that SOAR (a particular computational system for implementing cognitive models) is only one possible interpretation of Simon and Newell’s theory (Simon and Newell 1972) and not the only one as intended, so that it adds extra non-theoretical constraints into the implementation of models built in it.
2. The
system should make the process of translating the modeller's intentions into an
actual simulation as straightforward as possible.
This will never be a simple criterion to apply to a candidate ISSL, due to the presence of semantic complexity. However, steps can be taken to ease the process of implementation and document it. In general there should be structures in the ISSL that correspond as closely as possible to the basic items in the shared ontology of social simulators. This will probably change as the field develops. Presently, such a menu of structures might include: agents, models, scripts, utterances, time, norms, memes, groups etc. The trouble is that these entities are far from being theory-independent! Thus there is an inevitable tension between the ease of implementation and the wish for a computational base whose theoretical base is clearly separable from the focus theory. An approach to this problem is to provide structure for which there is most agreement and fewest issues of interpretation, which can be used to construct the others according to some intended (and hopefully documented) theory. Such structures might include relevant temporal scales, names, membership of recognised institutional structures, constraints upon action etc.
3. The
system should facilitate the introduction, definition and manipulation of
tokens and token structures that are readily interpretable in semantic terms.
At a minimum, the system should allow the definition of strings and their syntax so that they can be stored, manipulated and retrieved in a flexible way. Better, it should allow the use of lists, trees and other data structures of tokens in a relational way, so that it can directly represent a whole variety of linguistic and other natural structures. Ideally it should allow the specification and use of general expressions and their associated grammars so that the system can approximate some linguistic abilities.
4. The
system should encourage the identification, clarification, application,
manipulation and documentation of different types of constraints.
As far as possible the code that implements the different types of constraint should be able to be differentiated and labelled with the source of the constraint (as discussed above). It should be possible to determine the type of the constraint (e.g. hard, soft, warning, halt etc.) in relation to other constraints. For example, one might be more certain of some constraints than others, so if the simulation gets into a state where it will have to violate one or other of these constraints in order to continue, it will know which to transgress (but record this transgression).
5. The
system should allow for the controlled exploration of a specified space of
possible trajectories using a variety of means.
In most social simulations it is not intended that it predict a unique outcome, but rather pick one of a constrained range of possible trajectories. Quite apart from unintended sources of arbitrariness most simulations are intended not to be completely deterministic – uncertainty and contingency being essential aspects of many social systems. It is the intended constrained range of processes that is posited and explored using a simulation. For example, in the Schelling model, it is intended that the choice of which empty location to move to be arbitrary, but it is also intended that this arbitrary choice be constrained to the present location’s local neighbourhood. Once one has implemented the intended constraints, one then has to choose how to explore the range of possible trajectories that are left. Possibilities for such exploration include: a statistical sampling (e.g. Monte Carlo); an attempted enumeration of the space; the examination of example trajectories; or some calculation/proof of upper or lower bounds to the space.
6. The
system should provide tools for the flexible investigation and analysis of the
simulation outcomes to enable the development of an appropriate model of the
results.
As noted above, syntactic complexity means that it will be necessary to actively model the outcomes of a simulation in order to understand the results. In other words to find an appropriate viewpoint from which to analyse the outcomes and then the appropriate model of the outcomes from within that viewpoint. This process is frequently exploratory, so one wants to be as flexible as possible. In particular one should have a range of modelling tools (including numerical and statistical tools) and be able to apply them without prior restriction to a subset of the aspects of the simulation. In fact, ideally one should be able to iterate this exploratory process so as to enable the modelling of a model of the simulation outcomes, the modelling of a model of a model of the outcomes etc.
7. The
system should facilitate the construction of composite simulations where
different components can be developed separately and then brought together.
This is very similar to the requirement for effective encapsulation in computer science. Social simulators will often wish to incorporate mechanisms from a variety of sources into their models. An approach to this problem is to adopt object-oriented methodology and tools: strong encapsulation of objects which are instances of types which form a well-defined hierarchy. This still does not quite solve the problem when one wants to deal with inter-object processes or where one wants to import overlapping clusters of objects. Another recent innovation is to abstract patterns of solutions to frequent problems.
8. The
system should facilitate the understanding of the emergence of process.
Given that many social simulations are not constrained up to uniqueness and that social scientists are primarily interested in emergent process, an ISSL should not impose arbitrary constraints upon implementation. In other words, when implementing an intended specification one would not want to have to include extra constraints merely to make it run. Rather one would want to be able to specify the structure one wishes and explore the processes that are possible within this.
4. SDML as a step towards an ISSL
The computer language SDML (Strictly Declarative Modelling Language), was not developed with the above criteria explicitly in mind. However, it has been developed specifically to support social simulation, and has closely co-evolved with the CPM’s thinking on social simulation methodology — so it is not very surprising that it goes some way to meet the above criteria. As you will see in the next section the team that developed DESIRE …. In the last section of this paper we will make some tentative suggestions as to how we might go about pooling the knowledge gained by different teams to inform the development of the next generation of systems, but first we will look at each of the criteria introduced above and briefly outline how SDML goes towards meeting them. In each case I repeat the criterion for the convenience of the reader and then describe if and how SDML represents a step towards meeting the criterion.
1. The
system should be free of any particular social or cognitive theory. Whatever
theory exists to structure the system should be as clear as possible so that
its contribution can be cleanly distinguished from the intended content.
SDML has a logical basis and is therefore free of any particular social or cognitive theory. It is based on a fragment of Konolige’s Strictly Grounded Auto-epistemic Logic (Konolige 1992). This provides a clear semantics for SDML (i.e. a formal way for understanding and working out what it will do given certain rules). This basis provides an expressive base that allows the implementation of any computational representation of cognitive or social processes – the logic does not specify how an agent in SDML must think but allows any such process to be implemented. It is unclear the extent to which this logical basis is the most natural for implementing social or cognitive theories.
2. The
system should make the process of translating the modeller's intentions into an
actual simulation as straightforward as possible.
SDML provides some general and flexible structuring mechanisms. A model is composed of a number of interacting agents, which are objects with their own databases and rulebases. An agent’s databases record static and dynamic information about the agent (e.g. its perceptions or beliefs), and its rulebases determine its behaviour. Agents are arranged in a container hierarchy, with complex agents composed of simpler ones. Such composite agents can be serial or parallel, depending on whether their sub-agents are simulated in a sequence or (conceptually) in parallel with each other.
SDML also provides a flexible mechanism for the representation of time. Time levels can be defined, and these can also be nested inside each other. For example, a simulation may define the time levels week and day, with seven time periods at time level day for every week. The outermost time level, called eternity, represents information that is always true. Agents have separate databases for different time periods, with databases at more specific time periods inheriting from databases representing information that is true for longer periods of time. For example, something that is true for a whole week is true for every day within that week, and something that is true for eternity is true for every week. Agents can define additional time levels, allowing some agents to be simulated to a greater degree of temporal detail than others.
These two features mean that, to a significant extent, the structure of the simulation can be taken directly from the perceived structure of the social system being modelled. One can have institutions or groupings of individuals represented as whole entities, but also containing the individuals (or parts) that they derive from or cover. Each part of the simulation can have its own appropriate system of time: so a market might have a trading cycle whilst an individual might work within a finer level of time.
The container structure for the SDML implementation of the Schelling model is shown in figure 1. Each counter is represented as a sub-agent of agent schellingModel, which is a serial composite agent because the counters are simulated in a randomly determined order. An additional agent, called gridDisplayer is simulated after all the counters, to display the grid on the screen. Agent schellingModel has a single time level denoted iteration.
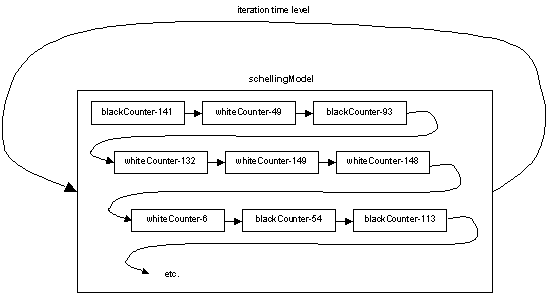
Figure 1. The container structure of the Schelling Model
In common with many other computer languages (the so-called “object-oriented” ones like C++) all objects, including agents, are defined as instances of types. Types are arranged in a type hierarchy, with specific types defined as subtypes of more general supertypes. Agents inherit information, such as rules, from their types, and subtypes inherit information from their supertypes. Types are gathered together in modules.
Part of the type hierarchy used in the SDML implementation of the Schelling model is shown in figure 2. The new types provided in the Schelling module are shown in bold; the others are some of SDML’s built-in types. Each counter is an instance of type BlackCounter or WhiteCounter, which are subtypes of Counter, which is itself a subtype of the built-in type Agent. This represents the knowledge that every black counter and every white counter is a counter, and every counter is an agent. Multiple inheritance is provided — the type SchellingModel (whose only instance is the agent schellingModel) is a subtype of both SerialCompositeAgent and LoopingAgent, giving it the abilities to simulate sub-agents in sequence and to introduce its own time levels. There is a clear correspondence between the elements of the social structure being simulated and their representation in SDML’s container structure and type hierarchy. This makes both structures straight forward to define. It should be noted that none of the built-in types are influenced by any social or cognitive theory, or are even specific to social simulation. In this simple model, it was fairly straightforward to write the rules of the various types from scratch. For more complex social simulations, it is useful to have predefined types corresponding to social entities. In SDML, this can be done by building up a library of modules containing such types. These modules are themselves arranged in a hierarchy, known as the module hierarchy. Types defined in a supermodule are inherited by all submodules. The root of the module hierarchy is the standard module, containing SDML’s built-in types.
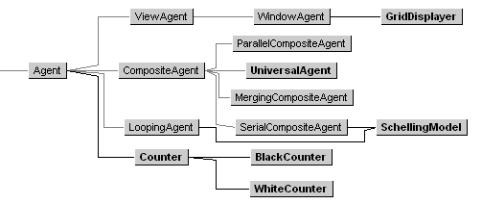
Figure 2. Part of the type hierarchy of the Schelling module
3. The system should facilitate the
introduction, definition and manipulation of tokens and token structures that
are readily interpretable in semantic terms.
In SDML, an item of information is represented as a clause on a database, consisting of a predicate and a number of arguments. For example, in the Schelling model, the knowledge that whiteCounter-42 is at position (5,7) at iteration 2 is represented by the clause gridCounter 5 7 ‘whiteCounter-42’ on the model’s database for iteration 2. The predicate gridCounter must be defined before it can be used. This is done using a clause definition, that includes, among other things, a syntax diagram for clauses with this predicate. The syntax diagram of gridCounter is shown in figure 3. As well as the types of the arguments, the syntax diagram specifies that there can only be one Counter in each grid location. In the above example, the clause represents a simple relationship between the tokens (objects) gridCounter and whiteCounter-42, and numbers. Clauses can also be used to build more complex data structures, since clauses can have subclauses. In the Schelling model, clauses are used for lists of agents and lists of points where each point is itself a clause. SDML has a few built-in types for data structures, including for lists, matrices and points, and the modeller can build other data structures such as trees and linguistic structures out of these basic constructs.
![]()
Figure 3. Syntax diagram of gridCounter
4. The system should encourage the
identification, clarification, application, manipulation and documentation of
different types of constraints.
An SDML rule is composed of an antecedent and a consequent. Every SDML rule is declarative and acts as a kind of truth constraint, specifying that if the antecedent is true, the consequent is also true. Rules can be fired, to infer that the consequent of a rule is true when the antecedent is inferred to be true. The antecedents and consequents of rules are clauses, which may contain subclauses and/or variables. Typically checking if an antecedent is true involves retrieving one or more clauses from a database, and inferring that the consequent is true entails asserting one or more clauses to a database.
In the Schelling model, each counter has a rule called “move or stay still” (inherited from type Counter) which specifies the counter’s current position based on its position at the previous iteration and the positions and colours of other counters in its neighbourhood. In effect the various constraints on the possible positions of the counter have been gathered together into a single rule.
SDML has some capabilities for constraint programming. A rule can be written which only fires under some assumption — whether that assumption holds can only be determined by firing further rules. One use of assumptions is in handling negation. The antecedent notInferred <subclause> is defined to be true if and only if the subclause is not inferred to be true (for any bindings of variables used within it). Inferences can be made based on this assumption, by asserting the consequent of the rule to the database tagged with this assumption. If the assumption later proves to be false (because the subclause or a subclause of the subclause is later inferred to be true), this inference is retracted. In order to fire rules efficiently, SDML partitions rulebases based on the dependencies between rules, and assumptions are resolved at the end of each partition. If there are no consistent resolutions for the assumptions in one partition, SDML backtracks to try to find other resolutions for assumptions in previous partitions. SDML also backtracks if false is inferred; i.e. a rule with false as its consequent is fired. Thus a rule with false as its consequent is a constraint that the antecedent is not true. However, this feature provides only limited constraint programming capabilities — such constraints can only be used to eliminate possibilities rather than generate them. Furthermore, this feature only provides one kind of constraint — hard ones that cannot be transgressed in order to continue with the simulation.
5. The
system should allow for the controlled exploration of a specified space of
possible trajectories using a variety of means.
Often, during a simulation, it is necessary to choose one value from a range of possibilities. SDML has several primitives, which can be used in antecedents of rules, to make such choices. These primitives include randomNumber to yield a random number in the range 0 to 1, randomList to yield a randomly ordered list, and randomChoice to randomly select one value from a set of possible values. There is also an arbitraryChoice primitive, which is similar to randomChoice except that the choice does not have to be random; any choice will do.
When one of the possibilities is chosen, SDML explores that trajectory. The backtracking facility described above can be used with the randomChoice and arbitraryChoice primitives, to make different choices and explore different trajectories if one trajectory leads to a contradiction (such as a constraint failing). There are two alternative primitives, called fixedRandomChoice and fixedArbitraryChoice, to make fixed choices that cannot be altered by backtracking.
In the SDML implementation of the Schelling model, there are three situations where such primitives are required. The initial grid is set up and the order in which the counters are simulated is chosen using the randomList primitive. When a counter decides to move to a neighbouring empty cell, it selects that cell using fixedRandomChoice.
Since the model is itself an agent, it can be embedded in a larger structure. This enables the same model to be iterated many times, and the results can be analysed using statistical techniques for example.
Because of SDML’s closeness to logic, it is likely to be more feasible than with other simulation languages to use a theorem prover to prove the bounds of possibilities within a model.
6. The
system should provide tools for the flexible investigation and analysis of the
simulation outcomes to enable the development of an appropriate model of the
results.
One of the features of SDML is an implementation of virtual memory. Instead of discarding databases from previous time periods, SDML writes them to a file and can read them back into real memory when required. This has two uses. Firstly, agents can analyse past data during the simulation, and secondly, users can analyse the data from outside the simulation.
The SDML environment includes a flexible query interface, allowing the databases to be interrogated in the same way as in the antecedent of a rule. SDML has limited built-in visualisation and statistical tools (such as displaying the results of a query in a graph or performing a linear regression). However, it does include a general facility to construct user interfaces (which is used in the Schelling module by the gridDisplayer agent to display the grid in a window on the screen). Also it provides the ability for arbitrary agents to work on past outcomes in order to model them (e.g. using a genetic program to summarise the behaviour of another agent in the simulation).
7. The
system should facilitate the construction of composite simulations where
different components can be developed separately and then brought together.
In SDML, different components can be developed separately in separate modules. They can be brought together by defining a new module which inherits from the component modules. All types, objects and rules, etc., defined in each of the modules are inherited by the new module.
Object-oriented encapsulation is provided using types. Clause definitions include readability and writeability attributes which can be used to restrict access to clauses on the agents’ databases. If the readability is private, internal or public, clauses can be retrieved by evaluating antecedents of rules in that agent, in that agent or another agent within it, or in any agent respectively. Similarly, the writeability affects where clauses can be used in the consequents of rules in order to assert to the agent’s databases. An object definition can also be encapsulated within a type, so that there are separate objects for every instance of that type. For example, an agent called gridDisplayer is defined in type SchellingModel, so if there is more than one model each has its own grid displaying agent. Each object is uniquely identified by a path which resembles an email address. In our example, the agent is gridDisplayer@schellingModel.universe. However, it can simply be referred to as gridDisplayer from within the schellingModel agent.
8. The
system should facilitate the emergence of process.
The declarative nature of SDML encourages the specification of facts and relationships, in terms of clauses on databases and rules. The process of firing rules in a rulebase is not specified explicitly. To some degree, the process emerges from the declarative structures of SDML. However, as in any declarative programming language, the process is implicit in the structures of the language and the mechanisms used to manipulate those structures.
For example, the order in which rules within a rulebase are fired is not specified by the modeller; instead it is determined by the system based on the dependencies between rules. Thus the order is implicit in the clauses used in the antecedents and consequents of those rules. In some cases, especially when assumptions and backtracking are used, the process of firing the rules is highly unpredictable and emergent to a high degree. In other cases, such as in the Schelling model, the process of firing the rules in a rulebase is highly predictable and emergent to a low degree (the properties that are particularly emergent are the longer term tendencies for counters to form clusters). It may also be noted that the order in which rulebases are processed is explicitly specified by the modeller (using time levels and composite agents).
There is a trade-off here between avoiding specifying process and obtaining sufficient efficiency. It would be possible to define a simulation entirely in terms of constraints and let the system resolve them. However, this is likely to be extremely expensive in terms of both execution speed and memory usage. SDML allows, but does not require, the process to be partially specified. Thus SDML facilitates the study of emergent process.
6. The Future of Social Simulation Languages
In this we would like to speculate a little bit, on the some of the features an ISSL might have in the near (if we are lucky) or far (if we are not) future. The first two subsections suggest that much greater support might be provided for the processes of mapping to and from social phenomena to the simulation. At the moment the processes are largely a “black art” and undocumented. Whilst we think it highly unlikely that this will be improved by a completely formal specification or analysis methodology, we do think that these mappings might be achievable in a more incremental and testable manner. The third subsection is more ambitious as it envisions a general modelling environment within which sets of simulation models can be held, run, manipulated and related.
6.1. The integration and management of the specification and implementation processes
In the specification and production of simulation models: the intention of the programmer; a specification of that program; the first prototype of the simulation; and an efficient simulation are all (or should be) strongly related. In particular a prototype of the program should be consistent with the specification of the program; and an efficient implementation of the simulation should exhibit the same outcomes as the prototype simulation. Generally the aim is to move in steps from general intentions to an efficient implementation: each stage being a specific case of the stage before. Thus a typical process might start from some prior knowledge about the social phenomena to be modelled (gained from expert opinion, ethnographic studies, anecdotal accounts etc.); choose or devise an abstraction of the phenomena that was consistent (or, at least, not obviously inconsistent) with that knowledge; compose a specification of a simulation to model a part of such an abstraction; write a prototype of the simulation to match the specification; then iteratively improve the efficiency of the simulation without changing its behaviour in the aspects that are relevant to the specification.
The ability to move from a descriptive specification to fixing (or otherwise constraining) some of the structure of the simulation within the same software would allow the provision of tools to capture and keep the motivation and intentions behind the specification. For example at each stage the programmer could choose a new constraint to place upon the model and be prompted to enter a comment about the reasons for the choice. The software framework could support alternative branches in this choice process along with the advantages of each. In the future a simulator (either the same one or another) could be aided in adapting the simulation by backtracking along the choice tree and choosing another branch.
Ideally the simulator would be able to animate the simulation in a rough and inefficient way at an early stage as possible. This might be achieved through a combination of the use of constraint programming techniques which search for a solution that fits loose constraints and the provision of stand-in proxies for unprogrammed parts (e.g. agents that take random actions from a menu provided). Being able to incrementally explore and specify the simulation might enable the simulator to focus down on the desired simulation behaviour in a way that was easier to understand, check and document.
6.2. Aids for the modelling and analysis of simulation outcomes
To understand the increasingly complex models that we use we have to model our models, either by postulating theories about the processes in those models, by graphing and visualising the results and by producing simpler models that approximate the emergent behaviour of the model. Sometimes we are even forced to model the model of our models. An example of this is when the simulator collects data from simulation runs which are, in turn, modelled in the form of a graph or approximated with an analytic expression.
Understanding our creations can be greatly aided by the provision of flexible query and data visualisation tools so that a researcher can interactively explore what happened (or is happening) during a simulation. Another tools is one that ‘fits’ analytic forms to the resultant data by finding the parameterisation that gives the lowest error of the form w.r.t. the data. In general, one would want to be able to ‘fix’ the first simulation as data and then use another simulation (or runs of a simulation) to model the fixed simulation. Here the first model simply plays the part of the validation data more usually used and the specification of the second meta-model coming from some hypothesis about the processes occurring in the first gained from inspection, visualisation and the like. Of course, there is no end to how far this can be taken in terms of meta-meta-simulations etc.
6.3. A software environment to aid the development of compositional models and the chaining of models
The above subsections are specific instances of a more general case: that of relating different but related models. We often need to compare models which are differently formulated but whose results are related. In fact we routinely use chains of models in our attempts to understand complex phenomena: starting with the data model and ending at quite abstract theories and descriptions. This was foreshadowed by Patrick Suppes when he said in 1960:
“… a whole hierarchy of models stands between the model of the basic theory and the complete experimental evidence. Moreover for each level of the hierarchy there is a theory in its own right. Theories at one level is given empirical meaning by making formal connections with theory at a lower level.” (Suppes 1960) p.260.
Thus we may have large chains or even clusters of models (as Giere (1988) characterises a theory) which are all interrelated by their content (i.e. their results).
In a typical simulation you might have the following related models:
1. the prior knowledge about the social phenomena with which you intend to make the simulation consistent with;
2. the intended abstraction of the phenomena which you will try to simulate;
3. the specification of the simulation;
4. the simulation code;
5. the simulation runs;
6. statistics, graphs or other means of interpreting the results;
7. a data model against which to help validate the results;
8. what the results correspond to in terms of the abstraction;
9. and a picture of what the results might correspond to in terms of the original phenomena.
Here one has nine interrelated models just for one “simulation”! Even if you do not have explicit accounts of 2, 3, 7 and 8 (which is, unfortunately, too frequently the case) that still leaves 5 interrelated models. A software framework which could hold and relate multiple runs of these some of these models would be very helpful. We describe a possible framework below.
The essence of a simulation is that there is some code that produces some results. It thus corresponds to a mapping between a space of possible programs and a space of possible results. Usually each run of the simulation traces out one ‘trajectory’ out of a set of possible trajectories that the code could produce. This trajectory is a concrete exemplar of the code. Thus the basic computational framework would need to hold the codes and some representation of the set of possible trajectories that the code could produce (conversely, that are consistent with the code). This is illustrated in figure 4.
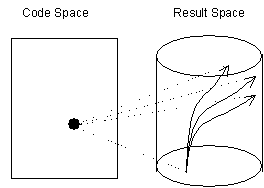
Figure 4. Simulation code corresponding to the trajectories from a set of runs
In figure 4 all the trajectories are shown as starting from the same state. This is not necessarily the case – in general a single program corresponds to a subspace of the result space. This subspace might be composed of a set of points, trajectories or even regions. Often we seek to characterise this subspace in terms of the trajectories central tendency and spread using statistics. Another way of characterising it is in terms of the ‘envelope’ surrounding the set of trajectories – which can be approached using constraint programming techniques (Terán et al. 2001). With the increasing complexity of subject matter and the increasing availability of computational power and data storage it will be advantageous to delay the simplification of data in terms of such descriptions as one might loose some of the qualatitative characteristics that later turn out to be important.
A data model (Suppes 1960) is one where there is a particularly direct relationship between the description of the model and what it corresponds to in the result space. This is not necessarily however a completely direct relationship because the data model might include indications about the accuracy of that data (as in “35±2mm”), in which case the description might map into a region of the result space or even a fuzzy region (if one is also including probabilities in this space).
It is occasionally possible to relate simple programs (or other formal models) using formal manipulations purely within the code space. This can occur when the operations in the code space have known effects on the result space. For example when a physicists approximate a set of unsolvable equations with a solvable set they use a lot of knowledge as to what changes in the formulae will result in results that are not changed to any significant effect. However in most cases, and with almost all social simulation models, this sort of move is completely impractical if not impossible. Usually the only practical way is to check the correspondence of models by their results.
There are two basic ways of comparing models by results, each is done by comparing sets of trajectories in some space of results (which is almost always a subspace of the total space of results). Firstly, one can say that the set of results from model-1 approximates the set of results from model-2. In other words there is some distance function from the two sets and this is acceptably small. If one such set is the data model which can been gained from target phenomena then we use measures such as the root mean squared error (RMSE) or the maximum absolute percentage error (MAPE). Secondly, one can say that the set of results from model-1 subsumes those from model-2. In this case the set of the trajectories from model-2 is a subset of those in model-1 (or using less strict criteria) that the envelope of the trajectories from model-2 is inside the envelope of the trajectories from model-1. These two methods of comparison are illustrated in figure 5.
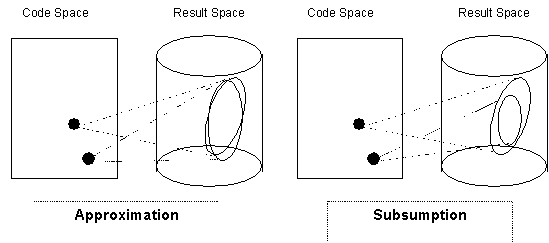
Figure 5. Comparing models via the result
space
(using the envelopes of trajectories for the purposes of illustration)
Of course it is possible that models might be related using different result spaces. Thus model-1 could subsume model-2 in result-space-A and model-2 could approximate model-3 in result-space-B. For example, model-2 might be a more efficient version of model-1 where there were fewer random choices in the simulation, so fewer trajectories could occur so that you could show in result-space-A (which might record the detail of the transactions in the models) that model-1 does subsume model-2. Then you might want to approximate some global outcomes of model-2 using an analytic model-3 in some space of aggregate measures of simulation outcomes (result-space-B). In this way you can get chains of models.
A particular case of this is where you have models of different granularities. One might have a detailed model of a farm and a coarser model of many farms in a region which one is checking against aggregate statistics of the agricultural output of that region. The model of the farm in the coarser model might far simpler than in the single farm model but be a good approximation of it in terms of actions with respect to the outside world (purchases, production etc.). Here the comparison is between a projection the multi-farm model by ignoring all but a single farm onto a result space of purchases and production. The coarser model would produce results that are intended to correspond with the aggregate statistics collected about the region. These model results would be compare to the aggregate statistics in a result space of the key statistical measures. A discussion of the use of validation at multiple grains can be found in (Moss 2001?).
Thus the envisioned computation framework would have the following features:
· the ability to store multiple descriptions including simulation code, data sets, and possibly other descriptions such as constraints on data;
· the ability to hold multiple simulation runs from the simulation code;
· the ability to define (maybe many) result spaces into which the simulation runs, data sets and constraints can be mapped;
· the ability to explore, measure and test the relationships between different subspaces in the result space;
· and the ability to annotate all these entities and the relationship between entities (such as the fact that a program is an elaboration of another program).
The single-farm, region of farms example discussed above within such a framework is illustrated in figure 6.
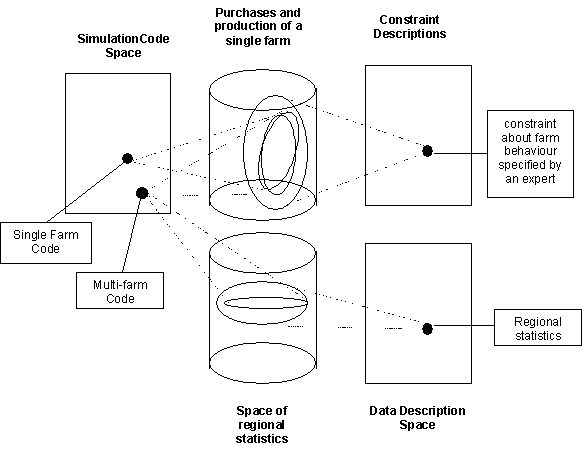
Figure 6. The farm simulation example within this framework
7. What Next?
Some possible future activities to move forward towards an ISSL include:
· The development of a Social Simulation Description Language which would provide appropriate semi-formal descriptions of social simulations that could be used in published reports of simulation so as to ensure that other researchers can reimplement them and try them out.
· Collaboration between groups producing future tools/platform for social simulation. This might includes software to enable social simulation to be performed on the emerging computational GRIDS or a joint successor modelling language to SDML and DESIRE.
· Establish norms within the social simulation community for judging a published social simulation model (e.g. as criteria as to publication). I have previously suggested some of these in (Edmonds 2000).
· Interchange of intended model structures and results in a more organised way (via a structured archive?).
· Establish flexible design methodologies for constructing social simulations and modelling the results, not in order to constrain these activities into a straight-jacket but so that fewer unintentional mistakes and omissions occur and that more of the assumptions, intentions and intended contexts are documented.
· Implementation of something approximating the multiple models computational framework as described above? (I wish!)
Acknowledgements
The thoughts herein are the results of discussion with numerous people: David Hales, Olivier Barthelemy, Richard Taylor, Juliette Rouchier, Catholjn Jonkers, Jan Treur and many others who I have forgotten. None of these are responsible for any mistakes. I also acknowledge the discussions with Scott Moss which are now so numerous that he can not remember whose ideas came from who[4].
References
Cartwright, N. (1983). How the Laws of Physics Lie. Oxford, Clarendon Press.
Cooper, R., J. Fox, et al. (1997). A Systematic Methodology for Cognitive Modelling. Artificial Intelligence 85: 3-44.
Edmonds, B. (1999). "Pragmatic Holism." Foundations of Science 4: 57-82.
Edmonds, B. (1999). Syntactic Measures of Complexity. Doctoral Thesis, University of Manchester, Manchester, UK. (http://www.cpm.mmu.ac.uk/~bruce/thesis/)
Edmonds, B. (2000). The Use of Models - making MABS actually work. In S. Moss and P. Davidsson (eds.) Multi Agent Based Simulation. Berlin: Springer-Verlag. Lecture Notes in Artificial Intelligence, 1979: 15-3.
Giere Ronald, N. (1988). Explaining science : a cognitive approach. Chicago ; London, University of Chicago Press.
Konolige, K. (1992). Autoepistemic Logic. Handbook of Logic in Artificial Intelligence and Logic Programming. D. Gabbay, C. Hogger and J. Robinson. Oxford, Clarendon. 3: 217-295.
Moss, S., H. Gaylard, et al. (1996). SDML: A Multi-Agent Language for Organizational Modelling. Computational and Mathematical Organization Theory 4(1): 43-69.
Schelling,
Thomas C. 1971. Dynamic Models of Segregation. Journal
of Mathematical
Sociology 1:143-186.
Simon Herbert, A. and A. Newell (1972). Human problem solving. Englewood Cliffs, N.J., Prentice-Hall.
Suppes, P. (1962). Models of Data. In Nagel, E. et al. (eds.) Logic Methodology and the Philosophy of Science: Proceedings of the 1960 International Conference. Stanford, CA: Stanford University Press, 252-261.
Terán, O., Edmonds, B. and Wallis, S. Mapping the Envelope of Social Simulation Trajectories. Multi Agent Based Simulation 2000 (MABS2000), Boston, MA, 8th-9th July, 2000. Lecture Notes in Artificial Intelligence, 1979:229-243 (2001).
Appendix — A Description of the Schelling Model of Racial Segregation
This model was originally described in (Schelling, 1971). We describe what we take to be its essence below.
Static structure
There is a large rectangular 2D grid of locations of fixed dimensions. Each location can be occupied by a black counter, a white counter, or be empty. Each location has a ‘neighbourhood’ of the eight adjacent locations (including diagonally). There are a fixed number of black and white counters on the grid, so that some of the locations are empty.
Temporal structure
There is a series of discrete time periods, starting at an initial period, over which the dynamics occur.
Important parameters
The number of black counters.
The number of white counters.
The width and height of the grid.
A parameter, C, between 0 and 1 for the proportion of minimum proportion of neighbours that must be the same colour in order to stay put.
Initialisation
The black and white counters are placed randomly on the grid at an initial time period so that there is at most one counter in each location.
Dynamics
For each counter, selected in turn, at each time period do the following:
1. Count
up the total number of counters in the neighbourhood, T.
2. Count
up the total number of counters of the same colour as the selected one in the
neighbourhood, S.
3. If
S/T is less than C and there is at least one empty location in the
neighbourhood, pick one such empty location at random and move to it, otherwise
stay put.
Results claimed as significant
There is a critical value for parameter C, such that if it is above this value the grid self-organises into segregated areas of single colour counters. This is lower than a half.
Intended interpretation
Even a desire for a small proportion of racially similar neighbours might lead to self-organised segregation.
Other details considered unimportant but which were necessary for the implementation
Size, shape and edge topology of the grid: the results can only be depended on when the movement of counters is not additionally constrained by the topology of the grid. This means that the grid has to be sufficiently large and not have a too extensive edge. Typically simulations have been performed on a 20x20 grid with the edges 'wrapped around' left to right and top to bottom, so that the surface has the topology of a torus and no edges.
The order in which the counters are selected: this does not seem to be significant, but either: counters are randomly selected individually; some order has to be imposed on the selection of counters (e.g. a randomly determined order); or some conflict-resolution method employed if they are processed in parallel and counters select the same location to move to.
The pseudo-random generator: this is used to decide the initial distribution of counters and the location to move to if there is more than one available. In fact, the results would probably still hold even with non-random generators as long as the movements occurred equally in all directions and were not linked to the selected counter's colour or the distribution of other counters on the board.
Source code
The source code for an implementation of this model in SDML can be found at:
http://sdml.cfpm.org/examples/schelling.sdm
This module requires SDML release 3.6 or later. For details of obtaining SDML see:
http://sdml.cfpm.org
Example output from running this code
