Abstract
We discuss the implications of emergence and complexity for the management of complex distributed systems (CDS). We argue that while formal design methods may play a role, they have distinct limitations where it comes to complex systems. There are similar limitations to statistical methods. Thus we must look to other ways of managing these systems, involving a shift from: prior one-off design towards post hoc continual management; from predictive abstract theory towards detailed descriptive modelling to guide monitoring and aid diagnosis; from system optimisation to simple disaster prevention; from single models to many models; from single well-designed mechanisms to multiple overlapping mechanisms; from individual to collective effort. We call upon those in the SASO community to explicitly reject those tenets that are only useful with simple systems. In other words, when trying to understand CDS, become more like zoologists rather than mathematicians and when managing them becoming more like farmers than engineers (at least in the classic sense).
1. Introduction
Consider farmers. They may know their animals, crops and land in some detail, but are under no illusion that designing a farm in advance would contribute more than a small part to its success. Rather they understand that they have to be acting upon it constantly to try and get acceptable results – less an exercise in careful planning than disaster avoidance using constant monitoring and mundane maintenance. In such a situation, new ideas cannot be assessed on the grounds of reason and plausibility alone (even those suggested by scientific advisors) but have to be tried out in situ. Solutions are almost never permanent and universal but rather a series of tactics that work for different periods of time in particular circumstances. Techniques that are seen to provide real benefit (even if that benefit is marginal) are adopted by others nearby so that, in the longer run, a community of specific and local practices evolve. This paper suggests that in order to effectively manage complex distributed systems (CDS) we have to learn to be more like farmers and less like mathematicians or engineers (in the classic sense).
This is a difficult lesson to adsorb. As computer scientists we are taught the value of good design – constructing the system sufficiently carefully so that we know that it will work well once built. That bugs are bad and we can limit them by carful specification and implementation. However CDS may not be very amenable to such an approach, requiring considerable and continual post construction adaption where the system is only ever partially understood. Here bugs may not only be inevitable, but the very things that make the CDS ‘work’. In other words learn to “farm” the systems that we need – system farming.
The argument proceeds as follows: Section 2 makes clear what we mean by the ideas of syntactic complexity, unpredictability and emergence, arguing that emergent phenomena cannot be formally reduced to system properties; ... in Section 6 calling on the SASO community to explicitly reject approaches that only work for simple systems.
2. Unpredictability and emergence
In this section we discuss and define unpredictability, complexity and emergence w.r.t. CDS. In particular, we want to show that: just because a particular emergent feature is caused by the mechanisms and set-up of a CDS and that each micro-step is completely understandable in a deterministic way, this does not mean that the emergent feature is reducible to the mechanisms and set-up. It may be that the assumption that “predictability” scales up from the micro to the macro is what lies behind much confusion in with respect to CDS. Rather, it seems that, as Philip Anderson put it, “More is Different” [1].
Complexity has many different definitions and meanings. This is because the complexity of a system is relative to the type of difficulty that concerns one as well as the frame/descriptive language in which that system is represented [7]. In this case we would characterise the syntactic complexity of a CDS as the “computational distance” from the set-up of a CDS to the resultant behaviour at a later point in time, that is, the minimum amount of computation necessary to determine a certain aspect of a CDS’s behaviour given the initial conditions, set-up, plans, programs etc. (this is similar to “logical depth” but without the condition that the program needs to be the shortest possible). If an easy-to-calculate short-cut to do this exists we say that this aspect of the CDS’s behaviour is simple. On the other hand if the shortest way to determine this is by running the CDS up to that point then it is (syntactically) complex. In the section below we will argue that many of the CDS that the SASO community deals with are complex in this sense.
Clearly syntactic complexity can make it infeasible for an actor/agent with computational limitations to predict future behaviour, even if it has the full details of the initial set-up and any subsequent environmental inputs. In particular, if we wish to be able to predict the behaviour of a class of such set-ups without simulating each one then the presence of such complexity makes this infeasible to do directly. Thus syntactic complexity can be cause of effective unpredictability. Pseudo-random number generators are an example of this in practice – their syntactic complexity makes their output unpredictable and arbitrary in practice.
Emergence occurs when some significant behaviour occurs that (a) is
not reducible to the details of the system set-up (otherwise it would not be
new), but yet (b) is totally consistent with those details (otherwise it would
not be from the system). Clearly both (a) and (b) being the case is impossible
within a simple formal system. Rather what tends to happen is: since in a
system of high (possibly infinite) syntactic complexity the behaviour is not
predictable from the set-up then observed behaviour that appears significant to
an observer is described in a different type of language to that of the
detailed interactions in the system. Since this description represents
observed behaviour of the system it will be consistent with its implementation,
but because it is in a different language, it will not be reducible to
descriptions of the implementation. For example, in Schelling’s model of
racial segregation [26] the implementation is in terms of counters on a
checkerboard and when they move, but the emergent behaviour that of the global
segregation observed as a result, even at high levels of tolerance
[13]. This is illustrated in Figure 1.
Figure 1. Emergence resulting from syntactic complexity plus abstraction.
3. Complexity in CDS
Emergence and unpredictability are inevitable features of complicated systems (including CDS), even if they are deterministic and perfect implementations of the programmer's intentions. This can be seen by looking at some formal systems which, although simpler than most CDS, can be easily mapped into them (i.e. they are a simplification of the CDS)
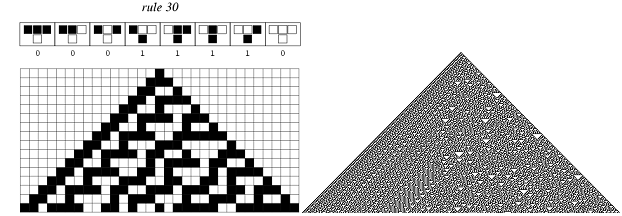
In
[27] Wolfram exhibits a Cellular Automaton (CA) which produces a
seemingly random binary sequence in its central column, in a deterministic
manner from a given initial state. Of course, since this is a deterministic
system and one has “run” it before with a particular initial state then one
knows (and hence in a sense can ‘predict’) what sequence will result, but if
one only knows what resulted from similar (but not identical) initial states
then there seems to be no way of knowing what will result beforehand. Of
course this is true of any pseudo-number generating program, the point is that,
in this case, it would be easy to design an CDS with the same properties using
essentially the same mechanism, so that what it had done in the past would be
no guide as to how it behaved the next time.
Of course it is very difficult to prove a negative, namely that there is no “short cut” to determining such a system’s behaviour without doing the whole simulation. So, despite the available evidence, it is always possible for people to simply assert that there must be some way of doing this. However there is formal evidence against such a hope in the form of Gregory Chaitin’s proof that there are mathematical truths of this kinds this kind whose simplest proof is as complicated as the truth itself [6]. For these truths there is no short-cut – no underlying, simpler reason why they are true. In fact Chaitin’s construction shows that all but a vanishing number of such truths are like this, so that those that are explainable by a simpler construction are the tiny exception. In other words, for most formal constructions there is no simpler explanation of them – they are not amenable to simplification.
[12] describes an apparently simple MAS, where agents have a fixed library of simple plans that pass unitary tokens between agents that is equivalent to a Turing Machine, and hence are unpredictable in general in advance as to their behaviour. In effect this system implements integer arithmetic which puts it beyond the scope of formal methods. Since most CDS involve processes such as arithmetic there will not be general and effective methods for predicting many of its properties. In particular as [12] showed there will be no general effective method for finding a program that meets a given formal specification (even if we know one exists), or a general effective method of checking whether a given program meets a given formal specification.
These sorts of results are basically versions of Gödel’s results [15]. In a sense Gödel’s results went further, they showed that (for most varieties of CDS) that there will be true properties of such systems that are not provable at all! That is that one might (correctly) observe properties of such a system that are not reachable in terms of a formal approach. In CDS terms that means that there may well be some emergent properties of deterministic systems as they run that cannot be proved within any particular logic or formal system. Similarly Wooldridge shows in [29] that, even for finite MAS the design problem is intractable (PSPACE complete).
Of course, the situation is even worse in the real world where there are essentially non-deterministic factors from a variety of sources, including: actions from actors/agents of unknown composition and goals, random inputs, chunks of legacy code which have insufficient documentation but are still used, bugs, and machine limitations. That computer systems of any complexity have unpredictable and emergent features, even isolated and carefully designed systems, is part of our everyday experience. That it is even more difficult to get complicated MAS systems to behave in a desirable way than traditional isolated and deterministic code is also part of our everyday experience.
Indeed Nick Jennings explicitly suggested that we stop MAS becoming too complicated in order to try and maintain the effectiveness of the design tactic. For example, in [22] his advice includes (among others):
• Do not have too many agents (i.e. more than 10);
• Do not make the agents too complex;
• Do not allow too much communication between your agents.
These criteria explicitly rule-out the kind of CDS that are studied in the SASO community as well as all those in any of the messy environments characteristic of the real world where they may be used. These rules hark back to the closed systems of unitary design that the present era has left way behind. What is surprising is not that such systems are unpredictable and, at best, only partially amenable to design-based methods but that we should have ever thought that they were.
4. Responses to complexity in CDS
So, given this situation, what can we do to try to get CDS systems to behave within desirable constraints? We consider some of the possibilities below.
The formalist answer is to attempt to use formal methods, i.e. proof, to make the engineering of CDS “scientific”.
[12] proved that formal methods are insufficient for the design of any but the simplest of CDS (e.g. those without arithmetic). Hence complete formal verification is only possible for the very simplest CDS components and almost no CDS that would help solve real world problems. However formality can help in some more mundane ways, namely:
1. Providing a precise and lingua-franca for engineers for specifications and programs (allowing almost error-free communication);
2. Allowing for specifications and programming to be manipulated in well-defined and automatic ways;
3. Facilitating the inclusion of consistency checks within code to prevent or warn of some undesirable outcomes;
4. Provide a stable and expressive framework/language for developers (or community of developers) to gain experience and expertise in.
What is important is to abandon the delusion that formal proof will ever be a major component in generating or controlling the complex system level behaviour that we see in real world problems.
The statistical approach is another way of getting at apparently disordered systems. The first step is assuming that the system can be considered as a set of central tendencies plus essentially arbitrary deviations from these. The idea is that although one might not be able to predict or understand all the detail that emerges from such a system this does not matter if there are some broad identifiable trends that can be separated from the “noise”. Thus far is fairly uncontroversial , but more problematic is the next step typically taken in the statistical approach, that of making assumptions about the nature of the noise, usually such as its independence, randomness or normality. That these are suspect for CDS is indicated by systems which exhibit “Self-Organised Criticality” (SOC) [3]. [23] list some criteria which indicate when SOC might occur. These are:
• Agents are metastable – i.e. they do not change their behaviour until some critical level of stimulus has been reached;
• Interaction among agents is a dominant feature of the model dynamics;
• Agents influence but do not slavishly imitate each other;
• The system is slowly driven so that most agents are below their critical states a lot of the time.
Clearly this includes many CDS. In such systems, one can not make the usual assumptions about the nature of any residual “noise”. For example when one scales up Brian Arthur’s “El Farol Bar” model [2] to different sizes and plots the variation of the residuals it does obey the “law of large numbers” as it would if it were essentially random. That is the proportion of the variation to the system size does not reduce with increasing systems size, as would happen if the residuals were random, but a substantial residual variation remains. This is shown in [8] which was suggested by the results of [24]. In this model a fixed number of individual’s have to decide whether or not to go to the El Farol Bar – basically they want to go if others do, but not if many others want to go. They make their decision in a variety of ways based upon the past history of attendance numbers. This sort of system results in a sharp (SOC) attendance patterns around the “break-even” point. The variance in this attendance is plotted in Figure 3 – one can see that this shows no evidence that the variation around the central tendency is dropping as a proportion of system size as the system gets larger. This means that the “noise” is not random and its distribution may well have undefined moments (which can invalidate many standard statistical techniques such as regression).
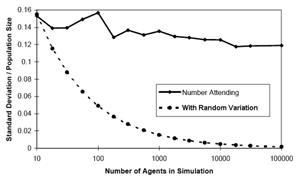
Figure 3. A plot of scaled standard deviation against different population sizes averaged over 24 runs over 500 cycles for each point in the El Farol Bar model [2].
The solid line connects the observed values; the dashed line what one would expect were the deviations were random. This is exactly the same sorts of lack of the law of large numbers that was found in [24] , which showed that in a globally coupled chaotic system what appeared to be noise did not diminish (as a proportion of the whole signal) with ever larger samples.
Here care should be take to distinguish between descriptive and generative statistics. In descriptive statistics one is simply describing/summarising a set of known data, whilst in generative statistics a data-generating process is encapsulated which is supposed to be a model of an observed data stream. Thus, in the latter case, there must be some sense in which the statistics are a model of the source of the observed data. So, for example, if one does have a SOC system which is producing a stream of data with no defined second moment, then positing a distribution with a defined second moment would be a fundamental misrepresentation. Whereas any finite set of data obtained from this source will have defined second moment, which might be a meaningful description of the data for some purposes (e.g. in comparison with a different set of data from the same source and with the same length). However it would be a mistake to interpret that statistic as representing anything about underlying system since it is merely an artefact of the fact you are dealing with a finite data set.
Due to the fact that one cannot rely on something like the law of large numbers means that one can no rely on the Monte Carlo method of averaging over multiple randomised runs of the system.
The infeasibility (and even impossibility) of using formal or statistical techniques to predict what a CDS will do based on fundamental principles leaves us with a problem, namely: what can we do to understand and manage CDS? This we turn to in the next section.
5. Towards Farming Systems
Dealing with CDS rather than simple systems will call for a change in emphasis. Below are some of the “axes” along which such a change may have to occur. This is a shift of viewpoint and approach – looking at the CDS as a given whole system. These shifts cannot be proved in general more than the indications from abstract cases (such as the ones above indicate).
5.1. Reliability from experience rather than control of construction
At worst many of the systems we will have to manage will not be those where we will have had control over its construction. These systems may be composed of a variety of nodes or components which participates within the overall system but whose origin is out of our control as with many P2P systems. Even if all the components are theoretically under our control in the construction phases this does not mean that this can ensure a reliable system in total, if the system is complex and adaptive.
In either case for CDS, trying to achieve system reliability by means of careful construction will have limitations, and some of the desired reliability will have to be gained via management as a result of us watching and learning how to intervene to keep the system going. That is using observation and experience of the system as it happens to be, rather than what it should be according to its design or construction. In a way this is a shift from a reductionist thinking about computational systems to a more holist one, as a result of a recognition that in practice (and often in theory) the detailed construction of a CDS is only a guide to resulting system behaviour. The construction may provide a good hypothesis for the system behaviour but no more than this.
5.2. Post construction care rather than prior effort
A consequence of the above a lot of the effort in managing CDS has to shift from before the moment of construction to after. No amount of care before a system is constructed will eliminate the need for substantial post-construction care and management. Instead of viewing our software constructions like a bridge whose parts can be largely relied upon and forgotten once in place, we may have to think of them more like a human organisation whose parts need substantial management once it is going.
5.3. Continual tinkering rather than one-off effort
Since parts of a CDS are constantly changing and adapting they will need continual adjustment. There may well be no permanent configuration that will be sufficient for the conditions it is to encounter. Instead of a one-off “heroic” effort of engineering, the more mundane activity of management and adjustment will be needed – re-engineering, adjusting and re-building parts as it is needed.
5.4. Multiple fallible mechanisms rather than one reliable mechanism
Since all mechanisms are fallible with CDS, multiple and overlapping systems can increase reliability, such as is found in biological systems. Thus if, for some unforeseen reason, one fails to work another might. That we cannot foresee that more than one mechanism will definitely be needed, we cannot tell that parallel and overlapping mechanisms will not be helpful. Rather a variety of mechanisms are more likely to cope with a variety of unforeseen circumstances.
5.5. Monitoring rather than prediction
CDS do not lend themselves well to prediction. If we could predict what they would do, we would be able to tell if our design was the correct one beforehand. It might well be that the best we can do is to merely catch trends and developments within a system as soon as possible after they start to develop. In this way ameliorative action can be taken as quickly as possible. The inherent unpredictability of many CDS means that we cannot be sure to detect it before it occurs (i.e. predict it).
5.6. Disaster aversion rather than optimising performance
The large uncertainties in CDS mean that one has no hope of optimising its performance (by any measure). Rather a more attainable target is simply the aversion of system breakdown. For example preventing the invasion of a file-sharing by uncooperative users, or distrust breaking a market-based system.
5.7. Partial rather than full understanding
CDS mean that we are never going to have a full understanding of what is happening, but we will have to be satisfied with partial or incomplete understanding. Such partial understandings may be fine for a certain set of conditions or context, but completely break-down in another set. Gaining a working partial understanding in a particular set of circumstances might be more important than attempting to achieve a full understanding. A continual partial re-understanding of CDS may just be more effective than spending a lot of time attempting a fuller one.
5.8. Specific rather than abstract modelling
The fact that some CDS are susceptible to sharp “phase changes” with changes of situation means that general and abstract models (or theories) of their behaviour may simply not be applicable. Rather we may can a greater handle on their brittleness and kinds of behavioural traits by modelling them in very specific and details ways – eschewing abstraction. This takes a lot more effort in terms of model construction but, on the other hand, it more straightforward since less abstraction is required – fewer decisions of what to include and what not to. A detailed simulation can be both a prototype of a system (so resulting global behaviour can be checked as well as its construction) as well as then being a (fallible) diagnostic tool once it is going.
5.9. Many models rather than one
The knowledge concerning the CDS may be incorporated in a number of simulations at different levels of abstraction. The lowest level being the detailed descriptive simulation described immediately above and higher levels modelling aspects of that simulation. Indeed there will typically need to be a series of simulations at different levels of abstraction. This multi-layered simulation approach was suggested in [9] (among others) and attempted in [20] , where a sequence of simulations models goes from the abstract to real applications. Similarly due to the changing nature of CDS with circumstance there will, almost inevitably, need to be a sequence of such models (or sequence of model chains), as the system evolves and develops.
5.10. A community rather than individual effort
Any effective working information about CDS will necessarily be detailed and specific to a particular set of circumstances. That means gathering many more examples, case-studies and evidence about the behaviour of CDS than it is feasible for an individual to collect. Thus those engaged with similar CDS being used in similar situations will need to pool their knowledge, spreading what does and does not work.
The short answer is that the understanding of CDS has tp become more of a "natural" (as opposed to formal) science – more like biology than mathematics or logic.
6. Conclusion
The wish for a “short-cut” to the production and control of CDS is strong, almost as strong as the wish for a “proper engineering” of CDS with firm foundations in logic and formal methods. But wishing does not make things true and one can only keep up the spin that we are “almost there” for a short period of time without substantive supporting evidence. It is now time to accept that managing CDS is fundamentally different from simple computational systems, that careful design will not be enough (or frequently even an option).
There is a place for design in the production and management of CDS, but it is not such a prominent one – rather the bulk of the progress will rely on trying out techniques and seeing which ones work, where they work and why.
In particular we call upon those in the SASO community to explicitly and loudly reject those principles and approaches that are not applicable to the systems they are working with (even though they may applicable for other, simpler systems). Namely to reject that:
• formal proof will play a major role in their production;
• there is likely to be any “magic bullet” techniques with universal applicability for designing CDS;
• the validation, management and adaptation of CDS are secondary matters that can be significantly ameliorated by good design;
• the specify and design methodology is the only real way to proceed.
Reading between the lines in many SASO papers that I have read, I think many in this community do reject these but have not openly declared this. However we argue that the SASO community will need to take a different path to that pursued by the agent community over the last decade, putting it in the vanguard of the “software revolution” detected by Zambonelli and Parunack[30] .
The nub is that we need to accept a more mundane role, the equivalent of a farmer. Less prior “heroic” design and more mundane post hoc management. Less abstract and general theory used to predict system properties and more specific and context-dependent modelling used to guide system monitoring and fault diagnosis. Less neat understanding and more of a messy “community of practice” using rules of thumb and models for particular circumstances and situations. Less assurance from good design and more from a history of having used and worked with such systems.
In a sense the whole of such conferences such as SASO are to explore how such farming can be reduced and/or eliminating as a result of intelligent design and deep understanding. This paper is simply a reminder that with CDS such efforts will be limited in their efficacy and that, if we are to develop effective means of managing CDS we might have to concentrate on the more mundane business of system farming.
References
[1] Anderson, P.W. (1972) More is Different, Science, 177:393-396.
[2] Arthur,WB; 1994, Inductive Reasoning and Bounded Rationality, American Economic Association Papers and Proceedings, 84:406-411
[3] Bak, P. (1996) How nature works: the science of self-organized criticality, Copernicus.
[4] Bennett,C.H. (1988), Logical Depth and Physical Complexity, in Herken, R. (ed) The Universal Turing Machine, A Half-Century Survey, OUP, pages 227-257.
[5] Caldarelli, G., Higgs, P.G., and McKane, A.J. (1998) Modelling coevolution in multispecies communities. Journal of Theoretical Biology, 193:345–358
[6] Chaitin, G. J. (1994) Randomness and Complexity in Pure Mathematics. Int. Journal of Bifurcation and Chaos, 4:3-15.
[8] Edmonds, B. (1999) Modelling Bounded Rationality In Agent-Based Simulations using the Evolution of Mental Models. In Brenner, T. (ed.), Computational Techniques for Modelling Learning in Economics, Kluwer, 305-332.
[10] Edmonds, B. (2005) The Nature of Noise. CPM Report 05-156, MMU, Manchester, UK. http://cfpm.org/cpmrep156.html.
[11] Edmonds, B. (2006) The Emergence of Symbiotic Groups Resulting From Skill-Differentiation and Tags, Journal of Artificial Societies and Social Simulation, 9(1) http://www.jasss.soc.ac.uk/9/1/10.html
[13] Edmonds, B. and Hales, D. (2005) Computational Simulation as Theoretical Experiment, Journal of Mathematical Sociology 29(3):209-232.
[14] Georgé, J-P., Edmonds, B. and Glize, P. (2004) Making Self-Organizing Adaptive Multi-Agent Systems Work – Towards The Engineering Of Emergent Multi-Agent Systems. In Bergenti, F. & al. (eds.) Methodologies And Software Engineering For Agent Systems, New York: Springer (was Kluwer Academic), 321-340.
[15] Gödel, K. (1931) Uber formal unentscheidbare Sätze der Principia Mathematica und verwandter System I. Monatschefte Math. Phys. 38: 173-198.
[16] Hales, D. (2000) Cooperation without Space or Memory: Tags, Groups and the Prisoner's Dilemma. In Multi-Agent-Based Simulation. LNAI 1979:157-166. Springer. Berlin.
[17] Hales, D. (2001) Tag Based Co-operation in Artificial Societies. PhD Thesis, Department of Computer Science, University of Essex.
[18] Hales, D. and Edmonds, B. (2003) Evolving social rationality for MAS using "tags", in Proc. of the 2nd Int. Joint Conf. on Autonomous Agents and Multiagent Systems (AAMAS 2003). Melbourne, Australia: ACM Press, 497-503.
[19] Hales, D. and Edmonds, B. (2004) Can tags build working systems? From MABS to ESOA, in Engineering Self-Organising Systems (ESOA 2003), LNAI, 2977:186-194.
[21] Holland, J. (1993) The Effect of Labels (Tags) on Social Interactions. SFI Working Paper 93-10-064. Santa Fe Institute, Santa Fe, New Mexico, USA.
[22] Jennings, N.R., (2000) On agent-based software engineering, Artificial Intelligence, 117(2):277-296.
[23] Jenson, H.J. (1998) Self-organized criticality : emergent complex behavior in physical and biological systems, Cambridge University Press, Cambridge lecture notes in physics: 10.
[25] Rao, A. S. and Georgeff, M.P. (1995) BDI agents: From theory to practice. In Victor Lesser, editor, Proc. of the 1st Int. Conf. on Multi-Agent Systems (ICMAS-95). MIT Press.
[26] Schelling, T.C. (1978) Micromotives and macrobehavior, New York: Norton.
[27] Wolfram, S. (1986). Random sequence generation by cellular automata. Advances in Applied Mathematics, 7:123–169.
[28] Wooldridge, M. (2000) Reasoning about rational agents. MIT Press.
[29] Wooldridge, M. (2000) The Computational Complexity of Agent Design Problems. Proc. of the 4th Int. Conf. on MultiAgent Systems, IEEE Computer Society, 341-348.