Simulation and Complexity
- how they can relate
Bruce Edmonds
Centre for Policy Modelling
Introduction
When faced with some complex phenomena for which we can see no adequate analytic approach, it is easy to produce a simulation model, play with it and feel that we have gained some purchase on it. However simulation models can often give the illusion of progress and understanding due to the persuasive nature. A key question is thus to what extent this is real progress and understanding and how much sophisticated (if unintended) deception, i.e. "Do simulation models really help us understand complex phenomena?"
Equation-based and statistical modelling have a relatively long history and are relatively well developed. Simulation modelling has a much shorter history and its methodology is less well developed. In many (but not all) fields academics are still feeling their way as to how and when to use simulation modelling. Further, just as there are many branches of mathematics, there are many kinds of simulation modelling. Within each domain it takes time to develop ways in which equations can be usefully applied, what sort of ‘leverage’ it can provide one, what the pitfalls are and how to go about it. A similar sort of development is occurring within many fields of study with respect to simulation modelling. What works within one domain may well not work in another. However, just as with applied mathematics there are some more general guidelines that can be discovered and communicated, and, just as with mathematics, how one applies the formal machinery is more of an art than a science. The knowledge about applying the technique is not entirely formalisable, but consists, for the most part, of ‘rules of thumb’, scientific norms, approaches and frameworks for thinking about what one is doing.
Thus part of the intention in writing this chapter is to draw some of this more general knowledge out and put it into some sort of framework. Its scope is where the domain of study is sufficiently complex that equation-based or other analytic approaches are impractical or even impossible to apply. This sort of domain poses its own particular kind of problems, which go beyond the difficulties or solving (or otherwise finding solutions for) analytical models. In such domains it is not possible to produce a complete model of the phenomena, rather one is attempting to model parts or aspects of the phenomena in useful ways. Thus I am not concerned with simple numerical simulation of well-validated equations here, but more the art and science of applying partial computational models. Inappropriate use of any kind of modelling generates more confusion than it sheds light but this is even more of a danger with simulation modelling applied to complex phenomena.
Three particular problems in this regard are as follows.
It is thus an open question whether a simulation models usefully inform one about some phenomena or whether they only give the comforting impression of doing so; simulation model is not a panacea but just another tool. I hope that in this chapter I will be able to sketch some guidelines to aid the useful use of simulation modelling and avoid the deceptive uses.
The chapter starts with an established and yet fairly simple account of the modelling process. This provides some of the reference for the terms and ideas to be used in the rest of the chapter as well as giving some idea of the nature of modelling and how it works. It then goes on to sketch some of what really happens when such models are applied in the process of research. This contrasts somewhat with what is presented in textbooks. The next section looks at some of the consequences when models are applied to complex phenomena. I then look at the problem of constraining our models, that is verifying and validating them. Finally I look at a neglected area: how a model comes to have meaning is not entirely clear. A successful predictive model with know conditions of application does not necessarily have any rich meaning. In the case of complex phenomena such black-box predictive models are rare and thus it is important to know what our models mean (and what they don’t) so that we have a better guide as to how to use them. All of this is illustrated with two example simulations developed at the Centre for Policy Modelling: that of modelling the interaction of mutual social influence on the domestic demand for water and that of integrating domain expertise with aggregate data in markets for fast-moving consumer goods.
About Modelling
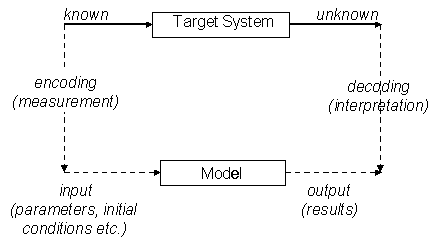
Any model is a model of something – what I will call the "target" system or phenomena. The model is some system which mimics certain aspects of the target via the model outputs. Something can not be a model on its own, one system is a model of another. Usually a model is parameterised (or relativised) via a set of parameter settings or model settings. These allow the model to be adapted to different cases of the same target. Before using a parameterised model one needs to set these "inputs" according to what these correspond to in the target system. Sometimes this involves a measurement process. The model is then run (or calculated) and the results (or outputs) can then be compared with those obtained from the target system outcomes. It is usual that there is some discrepancy between the model results and those representing the target system outcomes – this is the model error in this case. This account follows that of (Hesse 1963) and (Rosen 1978). These relations are illustrated in Figure 1 below.

Figure 1. An illustration of the basic modelling relations
This fairly simple relation between model and target can be compounded in many ways. For example the target could be a model of something itself; a model may be composed of sub-models; one model may be special case of another etc. I will discuss some examples of these later.
Simulation models can be used for many purposes, including:
In this chapter, I am primarily concerned with the last purpose, that of understanding parts of the world that we observe. There are (at least) three main ways in which simulations are used to do this, as: predictive; explanatory and analogical models. I will briefly look at each of these in turn.
A predictive model is one whose outputs correctly anticipate the relevant aspects of the target before these are seen by the modeller. The predictions do not have to be 100% accurate but simply accurately enough for the modeller’s purpose. What we gain from such a model are the predictions. The test of such a model is whether it can correctly predict unseen data that represents the target outcomes. It is not sufficient to merely validate such a model’s results against known data (e.g. dividing the data into in-sample and out-of-sample segments). The results of such a model can be used instead of the observations of the target, so that (for instance) one can plan for the effects before they occur in the target. Given that a model predicts it does not matter how it is constructed, or even be known why it works. However a successful predictive model naturally motivates a search for explanations as to these questions and is more useful when they have been answered. For example, knowing why and how a particular model correctly predicts may result in a more precise formulation of its conditions of application.
An explanatory model is one whose mechanism provides an explanation of how the results come about from the initial conditions in the target system. In order for such a model to provide an explanation, the structure of the model, the initial conditions and the results all have to be credible in terms of what is observed in the target model. What we gain from such a model is the candidate explanation of the workings of the mechanism that brings about the outcomes in the target system from the conditions from which it started (or why the outcomes came about from the initial conditions). A test of such a model is more complex than for a predictive model since as well as a match in terms of initial conditions and outcomes to known observations of the target system, the workings of the model have also to be credible. Otherwise the explanation that is the product of the exercise can already be ruled out. Of course, if the nothing is known about the mechanism any model which reproduces the appropriate outcomes for a range of initial conditions is a candidate, but in this case there may be many. On the other hand an explanatory model can be tested with known data. A popular way of doing this is to divide the data into in-sample and out-of-sample sections, to adjust the model with respect to the in-sample data and then check it matches the out-of-sample section to a sufficient degree.
An analogical model is similar to an explanatory model but is much looser. There is no test for an analogical model other than it seems useful for thinking about the target system. For this to be the case there has to be some correspondence between model and target but this can be complex and loosely defined. What an analogical model provides is some sort of guide for thinking (or experimenting) about the target, but it warrants no conclusions about the target that can be relied upon. This lack of definiteness does not stop analogical models being very useful, for example the planetary model of atomic structure is still used as a way of envisioning the electronic structure of an atom regardless of its many inaccuracies. If there is not a good explanatory model for some mechanism then we will often make do with an analogical one. However, analogical models can be misleading – it is easy to get so used to thinking in terms of a particular framework of analogical models that one mistakes it for an explanatory or even predictive model.
How good a model is depends upon one’s purpose in constructing or applying that model. However some criteria that are more generally looked for in a model can be explicated. The relative importance of these will vary depending on the situation and the modelling purpose. I will briefly discuss five of them in turn, namely: the soundness of the model design; its accuracy; its generality; its simplicity; and its cost.
In any particular modelling situation there will be trade-offs between these criteria. Achieving one may mean doing less well at another. Thus for example, it may be possible to ‘fit’ a particular set of observations better by elaborating a model or by abstracting away from a descriptive realism achieve a greater generality. There are no universal rules governing these trade-offs but it does seem that a single-minded quest for perfection in one or two of them often tends to result in deterioration in the others. I illustrate a possible four-way trade-off in Figure 2 below.
For example, philosophy could be characterised as the search for (usually linguistic) models that are immune from possible counter-examples, however strange. This means that they aim for complete accuracy (i.e. zero error) and complete generality (there is no special case where it does not hold). A result does seem to be that their models are either simple and vague or specific and extremely complex (or both vague and complex). To take a different example, a data model, i.e. a model composed of a set of observed data points (Suppes 1962), achieves simplicity, accuracy and specificity but has not generality at all. A third example is that of a model that encodes the equivalent of "anything may happen" – this may be simple, completely general and without error but is not at all specific. In general all the most useful models seem to lie somewhere in the middle, neither ultimately specific, accurate, general or simple, but nonetheless a useful compromise.
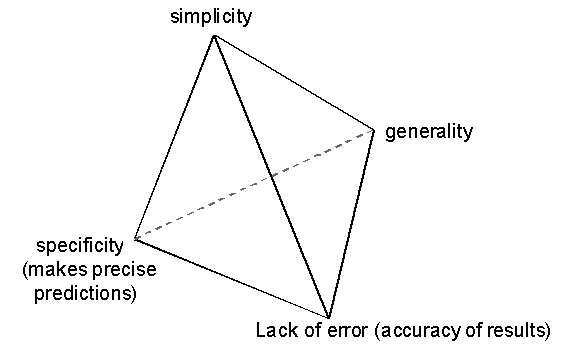
Figure 2. An illustration of a possible set of modelling trade-offs
Chains of Models
It is rare that a modelling situation is as simple as suggested in Figure 1 above. For example, it often occurs that a ‘data model’ is used between the observations and the main model (Suppes 1962). That is a series of measurements or other observations are recorded about the phenomena, and it is this series that is then related to the model. The series is a basic kind of model itself, a data model. Unsurprisingly data models are more frequently used in conjunction with explanatory models than with predicative models (which are easier to directly relate to the phenomena via their predictions).
Another common occurrence is that there are two kinds of model: a "phenomenological model" and an explanatory model (Cartwright 1983). A phenomenological model directly relates the data representing the phenomena, it is frequently a predictive model. The explanatory model is more abstract and acts to explain the phenomenological predictions made. It may, in turn be situated within a general theoretical framework or theory, such as Newton’s laws of motion. This is illustrated in Figure 3 below.
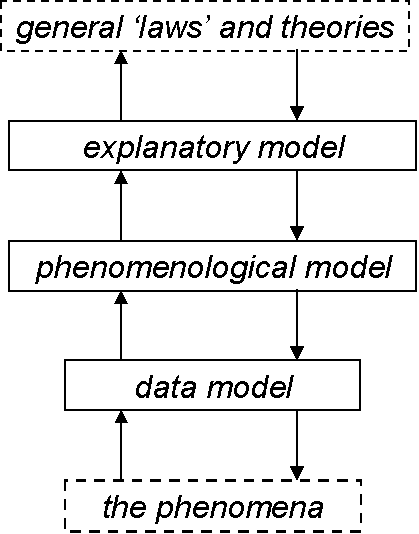
Figure 3. An illustration of models layered by abstraction
An example of this is relating volume, pressure and temperature of a gas. The phenomena may be a sealed but expandable container of gas, which at different times has different volumes, temperatures and pressures. At many instances simultaneous measurements of these three properties are made and recorded into a fairly comprehensive set of data – the data model. The gas laws successfully model the relation between these triples of data, so that at the same pressure the volume is proportional to the temperature (measured from absolute zero). However the gas laws simply relate the phenomena, they do not explain why they are so related. A model of the gas composed of a sparse collection of molecules, can explain the gas laws, when the speed of the particles is related to the temperature. Using some judicious approximations one can derive the gas laws from this model. This model explains why temperature, pressure and volume are related, but does not itself express the relation between them – to infer these relations one needs extra assumptions. The mechanics of the particles in this model are consistent with Newton’s laws of motion and the theory of the nature of temperature.
An ideal gas is an exceptionally simple case, where the phenomenlogical law can be obtained from the partical-based model using judicious assumptions of randomness, due to the lack of any significant interaction between its parts. In many other cases there is no adequate analytic approach to the modelling of molecule interaction – the only way to do this is via extensive simulation. This approach is discussed in (Gunsteren and Berendsen 1990) and the relation between the models illustrated in Figure 4 below.
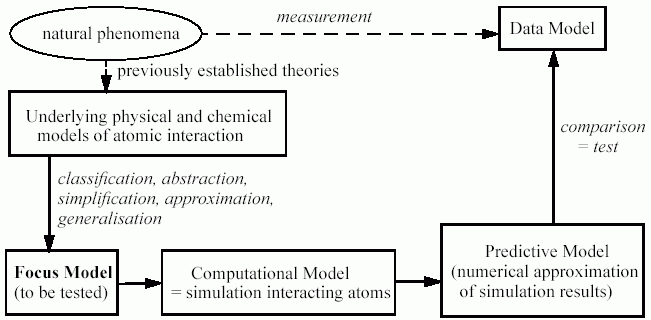
Figure 4. A layering of models in chemistry adapted from that in (Gunsteren and Berendsen 1990)
In this case the focus model concerns how a set of atoms interact (e.g. how the molecules pack or move in a certain state), this can be simulated using a representation of a set of atoms in 3D space using model of the underlying atomic processes. The simulation is run a great many times so that a summary of the results can be obtained by averaging etc. These results are further summarised into an equation that approximates the results, which is then compared to many different sets of measurements of the relevant natural phenomena.
3. Consequences of modelling complex phenomena
When modelling complex systems and phenomena, not only are more models going to be required but each of the models will need to be more complex. The presence of complexity and chaos means that the detailed interactions of a system’s parts can make a significant difference to the outcomes. If this is the case then a formal model that captures this detail is likely to be analytically intractable. If it is made tractable by the use of suitable ‘averaging’ (or other) assumptions or approximations then it will loose the causal link between the detail of the interactions and the outcomes, and thus cease to faithfully capture this aspect of the phenomena. However if one does not produce such tractable meta-models one is reduced to numerically simulating the model in order to get any results. Thus any model, regardless of whether it is expressed as an equation-based model, it is effectively a simulation model. A detailed simulation model that is more descriptively accurate, i.e. that captures the detail of the processes involved, may be far more preferable than a ‘general’ analytic model that smoothes these away.
Model complexity is not a single property, rather there are many ways in which a model can be complex (Edmonds 1999b). I consider two: what I call ‘syntactic complexity’ (immediately below), and ‘semantic complexity’ (in a later section).
The syntactic complexity is the computational ‘distance’ between the set-up of a simulation and the outcomes. A greater syntactic complexity means that a lot of computation is necessary in order to produce the outcomes from the initial specification – there is no effective ‘short-cut’ by, for example, ignoring some of the details. An example might be an evolutionary system: the initial set up is the set of individuals and the environment and the outcome is what behaviour they eventually evolve – the only way of finding out what behaviours can actually evolve is by running (or simulating) the whole system. This idea is illustrated in Figure 5 below.
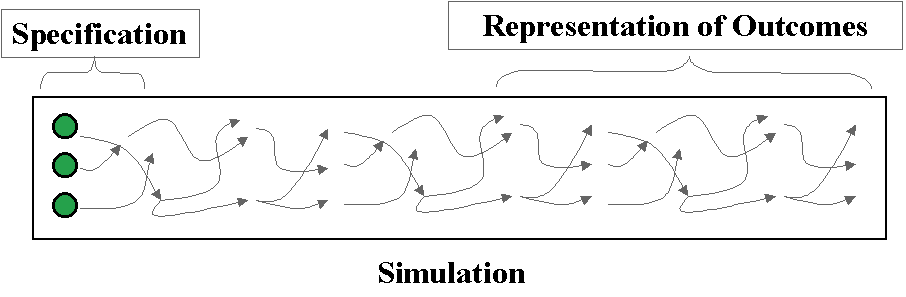
Figure 5. The computational ‘distance’ between the specification of the model and a representation of its outcomes
A consequence of syntactic complexity is that there are at least two separate views of the system, a description of the set-up of the system (a specification) and a description of the outcomes at a relevant level – the representation of outcomes. Sometimes there is a high-level explanation (or model) that relates the specification to the representation of outcomes, so that one can understand why the outcomes result from the specification at an appropriate level without having to go through the detail of the simulation execution. For example there might be some "pressure" built into the design of the simulation that results in a definite tendency in the simulation - when the simulation results in this tendency being statistically apparent this is not surprising and can be explained without reference to the precise detail of the computation (which may be difficult to explain). In other cases, where there is no bridging model that explains an appropriate representation of outcomes from the initial specification then we may say that these outcomes are 'emergent'.
It is likely that there will be many different ‘views’ associated with a simulation. There may be more than one relevant representation of outcomes, and indeed several abstractions of these representations. There may be more that one theory or model that links the specification to the representation of outcomes. Finally there may several analogies which might be applied to thinking about the simulation. These different views of a simulation are illustrate in Figure 6.

Figure 6. Some different views of a simulation model
The conclusion of all the above sections is that there are going to have to be many more models, each of which may be somewhat related to other models in complex 'model clusters' (Giere 1988). Solitary models of unitary design will be the exception rather than the rule. Figure 7 shows an example model cluster where there are two simulation models: one of a single farm and one of a set of interacting farms. The single farm results must be consistent with descriptions of farm behaviour gained from a suitable farmer; the code of multi-farm model is composed of several instances of the single farm model; and the results from the multi-farm models approximate to the regional statistics concerning farm output.
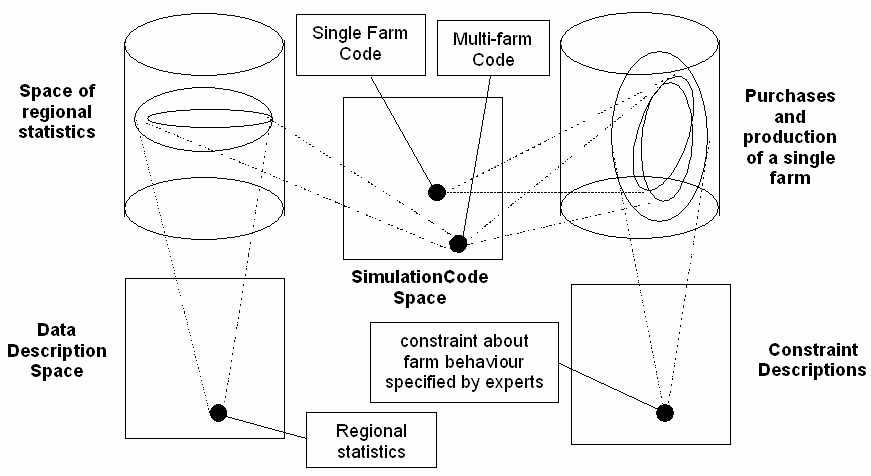
Figure 7. An example of a cluster of related models
4. Constraining Our Models
There are so many possible models that the main problem is not usually how to construct a model, but how to constrain the myriad possibilities down to something useful. The trade-offs briefly discussed above indicate different ways in which we can select which models we use. Each of these can be seen as a (partial) constraint on acceptable models – they are the reasons why we may reject models which are not good enough for our purposes. Such constraints are of utmost importance in model construction, and in simulation models in particular, for they may provide the justification for the model. This problem is particularly acute with simulation models (and even worse for agent-based simulation models) – these kinds of models typically need many more constraints than some traditional equation-based model forms (e.g. linear regression models).
These constraints can be broadly into those constraints which act upon the model design before the model is used and those which give the criteria for judging whether a constructed model is good enough after it is used. The former I call a priori constraints and the later post hoc constraints. I discuss each of these in turn.
A prior constraints act on the design and construction of a model and can include: known information about the phenomena being modelled; what model types are known or traditional; which models are consistent with well-validated frameworks; expert or stakeholder opinion; anecdotal evidence; constraints in terms of what is thought to be feasible in terms of cost and effort; which kinds of models will give one the answers one wants; and the uses the models are to be put to. These constraints have different sources: beliefs; knowledge; theories; analogies; observations; uses; and limitations due to circumstance. These sources themselves will have different origins and will have acquired their status in different ways: some will have social origins; some come from tradition; some will have been validated by previous experiment or use; some will be essentially arbitrary; and some will be because no other way was thought of.
Post hoc constraints act on the results or as a result of the use of a model and can include: the accuracy of the results as compared to a set of data (i.e. the error); the consistency of the results as compared to the results from other models and observations; the consistency of the results with expert or stakeholder opinion; the speed with which model a produces results; and the amount of space the results require. These constraints can be applied at a variety of granularities – thus they can be applied at an aggregate level, or at a level of each individual or variable in the model; they can be applied to average levels over time or finely at each instance of time in the results; and they can be applied to aggregates over a large number of runs or to each run separately. (Axtell and Epstein 1994) define a number of different levels of agreement of a simulation model with its target on this basis. Finding the appropriate level at which to make these comparisons is far from trivial – the fine detail of results may well not be informative as the model may have employed a random proxy for some arbitrary events, but looking at the results at a level that is too aggregate may miss the important details.
A particular example is the contrast between models that are designed to reveal a state (usually a final or equilibrial state) and those that are designed to reveal a process. Many equation-based models are designed to calculate a resulting state, partly due to the fact that analytically-solvable equations are more suited to this sort of task. Simulation models, on the other hand, are ideal for investigations as to the sort of processes that may results from a given system set-up, since they incrementally calculate their results and these results can be easily manipulable for exploration, visualisation and analysis.
When one has chains or clusters of models as discussed in the previous sections, the constraints for one model may well originate from one of the other models. Two principle kinds of these constraints are those of verification and validation. Verification is an a priori constraint, where one model’s design is constrained so as to be consistent (or otherwise informed by) a previous or well-established model. Validation is a post hoc constraint that the results are reasonably in accord with the results of another model. Thus in the chemistry example above the interaction between atoms in a focus model may be verified with respect to a model of atomic interaction, and its results (indirectly) validated against sets of measurements taken of the phenomena.
Some of the positions in the philosophy of science can be recast in these terms. Popper (1968) argued that a priori constraints are not enough but that models must be amenable to being selected out by post hoc tests (preferably ones rooted in evidence). Feyerabend (1975) argued that there should be no a priori constraints imposed on model construction (especially not those derived from tradition). Realism can be seen as the thesis that models should be narrowed down to (near) uniqueness by constraints derived from observations and measurements of phenomena, constructivism as the thesis that a priori constraints and sources not rooted in observations of phenomena are inevitable and unavoidable in the construction in models because they can not be constrained to uniqueness from observations alone. In a sense this framework deflates the realist-constructivist divide into a matter of degree – the degree to which observations constrain our models and the degree to which we are free to choose our own constraints in any particular modelling situation. Kuhn’s "theoretical spectacles" (Kuhn 1962) can be seen as the inevitability of using a strong existing a priori framework to design models and select the data models used for post hoc constraints.
It does seem to be impossible to do away with a priori frameworks and starting points altogether, and it is often difficult to completely disentangle which constraints are tainted by unquestioned assumptions and which are faithful reflections of the phenomena under study. However, whether you are a realist or a constructivist, it is always good practice to make the constraints used as explicit as possible. In this way others revisiting the model can make a fresh judgement as to the type of constraints that were used and thus be able to use (or avoid) the model as appropriate. Thus, although we can never know for sure that we not overlooked some assumptions, we can make sure that as far as possible we make our assumptions and sources explicit and document them adequately.
5. The Meaning of Our Models
The last aspect of modelling I will discuss in general is the matter of the meaning of our models. This is particularly pertinent for simulation models which are by nature more suggestive of interpretation than, say, analytic equation-based models. This has important positive as well as negative consequences. Simulation models can represent complex phenomena in a relatively rich and intuitive manner. The separate parts of the simulation can be representative of the corresponding parts of the target system and can develop in the simulation in a similar way to how the system develops over time. Such a correspondence allows for the animation of the development and interaction of the parts so as to be immediately interpretable and critisable. In this way simulation models can have a semantic role, as a medium of communication between stakeholders and other interested participants far beyond the closed realm of the expert modellers. Developing and exhibiting such a model can have immediate personal and political significance. I know of one case where researchers into water flow in a certain French river basin are not allowed to develop and publish models of flooding due to the political fallout of making vivid and believable that floods may occur at certain places in the valley. This seems far from the formal scientific use of models, but will become increasingly significant as simulation models become more prevalent.
The semantic and formal uses of models may seem to sit uneasily with each other, but these two aspects have always been with us. The job of an explanatory model is to give a meaningful explanation for some phenomena, whilst a predictive model does not have to. Whilst it may be that some philosophers of science in the middle of the 20th Century may have wished to reduce modelling to a purely formal function, it is now increasingly clear that this is neither possible nor useful (Morgan and Morrison 1999, Cartwright 1983). However just because models (and simulation models in particular) can have both aspects does not mean we should conflate or confuse these aspects – an explanation is not the same as a prediction and however suggestive a simulation is we should not rely on it in the same way as one might rely on a successful predictive model. Likewise it can be tempting but misleading to interpret the mechanisms inside a predictive model as having any meaning in terms of the workings of what is modelled solely on the grounds that it is successful at predicting. Thus some examination of how models acquire (or lose) meaning may be helpful in avoiding such traps, without simply denying the existence or usefulness of either aspect.
All models are constructed and applied in specific contexts. A lot of the meaning that a model may be attributed will be in relation to these contexts. To the extent that a model is abstracted away from specific contexts it will lose the possibility for rich semantic meaning and take on a restricted and more formal role. This has been the ideal in much of science; models should be abstract, formal (in the sense of being syntactically manipulable), and as generally applicable as possible. Models that are linked to more specific contexts, that have richer semantics and have more limited conditions of applicability have been treated as more suspect.
What I call ‘semantic complexity’ is the difficulty of completely capturing some phenomena in a formal system (like a computer simulation). The theoretical arguments for the existence of such phenomena is not relevant here (for this see Edmonds 1999a), however it is certainly true that many phenomena are not completely capturable in practice for the foreseeable future. Thus regardless of philosophical arguments this is a real factor with any actual model.
The existence of semantic complexity in practice has several consequences for the exercise of modelling. Models of such phenomena need to be less ambitiously general. That is, such models are only acceptable within a restricted scope - they have a more limited applicability. Secondly it will be very difficult to abstract very far from the phenomena being modelled, the models will have a more descriptive flavour. Finally, since each model will only be adequate for certain aspects of the phenomena, one may well need a different model for each purpose or aspect one is concerned with. One is likely to have different models for different situations and contexts, with only cautious generalisation away from these.
Thus in complex cases, more care is needed to ensure that models are not applied in inappropriate contexts, since the models will have a restricted range of applicability. It is almost always impossible to include all possible causes in a model; constant or irrelevant factors are usually omitted as ceteris parabis conditions. These ‘background’ assumptions that are omitted can sometimes be abstracted, recognised and labelled as a ‘context’. In order to be able to apply such a model in a different context from the one the model was developed in, it must be possible to recognise when the same set of background conditions hold. The ‘fuzziness’ and complexity of the context recognition enables models to be expressed within the context in relatively simple and ‘crisp’ terms. If the precise conditions under which the model could be applied were able to be formalised, then it could be included into the model itself allowing the model to be generalised. However this is not usually possible, for getting a complete set of conditions is an indefinite task – there can always be unnoticed background assumptions that are not articulated. The best we can usually aspire to is to sometimes formalise some of these background assumptions but not all of them. There is a growing body of evidence that such context-dependency is deeply embedded in human cognition (Suchman 1987, Davies and Thomson 1988, Clancy 1997), but that we are so good at mentally ‘flipping’ between different contexts that we are not aware of it. For more about context with respect to modelling see (Edmonds 1999c).
How meaning (in the sense of linguistic meaning) is ascribed and recognised is not well understood. However a credible account is that meaning is bootstrapped from use in specific contexts and established and corrected in conversation (i.e. Wittgensteinian ‘language games’). Thus there is a danger that the meaning of a model will be misunderstood (or misapplied) when applied out of this context. Like an analogy the meaning of the model may be helpful in the new context but, equally, may be misleading. For this reason, if a model has semantic aspects in the form of rich meaning (for example, as part of the conceptualisation of a domain which is being negotiated about) then it can not be assumed to retain this in a new context (say a new domain of negotiation). However if one stays within the same context this aspect may be developed with great effect and be very useful to the participants who use it. Such models may have a mixture of formal and semantic validity without too much danger of confusion, but only if they remain in context. This contrasts with the validation of the syntactic aspects of models which are validated via data models of phenomena gained via a measurement process. Many simulation models have some of both these aspects – some aspects are validated against data and some are validated against opinion.
In contrast to the situation where a model aquires it own meaning by use in context, meaning may simply be imported into a model in the form of natural language fragments (or other representations) which already have an established meaning. These fragments may be used as ‘syntactic sugar’ for the more formally labelled parts of the model or they may be manipulated as a result of a simulation run. In either case they reappear when presented as part of the results. Such labelling usually represents the intention of the modeller as to what the parts of the model represent. The labels act to suggest the interpretation of these parts. This has obvious dangers in that it can be misleadingly suggestive. The way that the labelled parts of the model relate to each other can, however, be validated against expert or stakeholder opinion. That is, the story it suggests can be run past experts who can say whether it is credible. Clearly there needs to be enough of a relation between the model and the target phenomena so that the suggestive labels are presented in the results in a way that is comparable to how what those labels stand for in the phenomena relate to each other. This can be ensured if the model is embedded in a tight interactive loop with the relevant experts or stakeholders, so that the model can be continually corrected and can truly enter the discourse in its own right.
In quite a few simulation models the relation to the target phenomena is indirect. That is, the computational model does not directly relate to the domain (either syntactically or semantically), but only to a conceptual model in the mind of the modeller. This conceptual model is the way that the modeller thinks about the phenomena – indeed in many cases it seems that quite a few modellers conflate their conceptual model and the phenomena itself so that a successful model of their ideas are taken as an adequate model of the target phenomena. This relation is shown in Figure 8. At worst the result can be that what is basically a representation of a set of ideas is mistaken for reality and conclusions projected upon that reality; at best the conceptual model is clearly delineated, the model is used to enrich and critique the conceptual model which is then used by itself in dealing with the phenomena of interest in an appropriate manner. This is discussed in more detail in (Edmonds 2000).
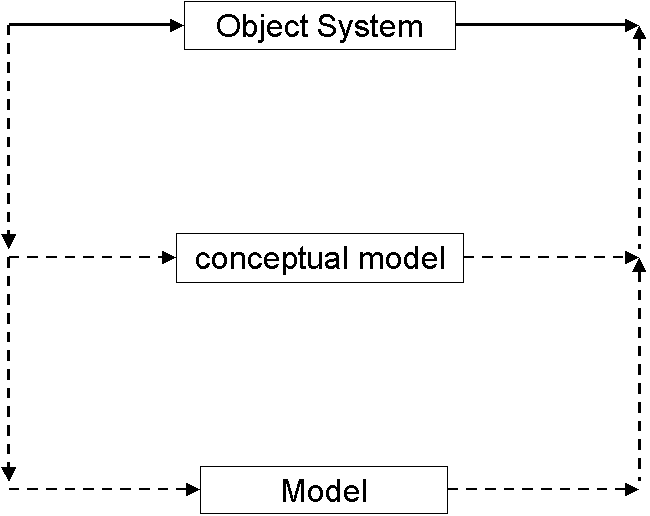
Figure 8. Indirect modelling of complex phenomena via an intermediate (and often unarticulated) ‘conceptual model’
Clearly the relative ease with which computational models can be built (compared with, say, equation-based models) and then used to convince others of their results has inherent dangers. However this is similar to many techniques developed by science (e.g. statistics) – after an initial credulous period people adapt to the technique and start to treat it with a healthy scepticism.
6. Example Simulation Models
Here I briefly present two models that I have been involved with, where the phenomena being modelled (and to a lesser extent the model itself) are complex and where the model has semantic as well as formal aspects.
Example 1: a model of social influence and water demand
This simulation model was to investigate the possible impact of mutual social influence between households on patterns of domestic water consumption. This was in the context of a larger project, The CC:DeW project to estimate the effect of climate change on water consumption in the UK. The model and the larger project are described in more detail in (Downing et al. 2003). The aim of the simulation model was to generate some possible collective outcomes, that is the simulation should produce behaviours that interact in traceable ways so that in aggregate they will be comparable to known water demand patterns. Thus the model was designed so that the structure and household behaviour are deemed credible by relevant experts; the ownership and use of appliances have the characteristics indicated by survey data; and the aggregate demands are similar to the kind of water demand patterns observed.
The basic structure of the model is illustrated in Figure 9. There are 100 households which each have a number of water-consuming appliances, such as showers, washing machines etc. These are used with a frequency and volume indicated by statistics from real households. Each household is amenable to influence from a number of sources: from neighbours (particularly the neighbour most similar to themselves); from the policy agent (either the local authority or water company); and what is available to acquire as new purchases. All the policy agent does is to recommend reduced water consumption during droughts (the recommendations get lower as a drought continues). It does this when the ground water is dry for a set amount of time, which is based upon an established ground water model which has rainfall and temperature as its basic inputs. The water demands of all the appliances in each household are summed to give the aggregate water demand.
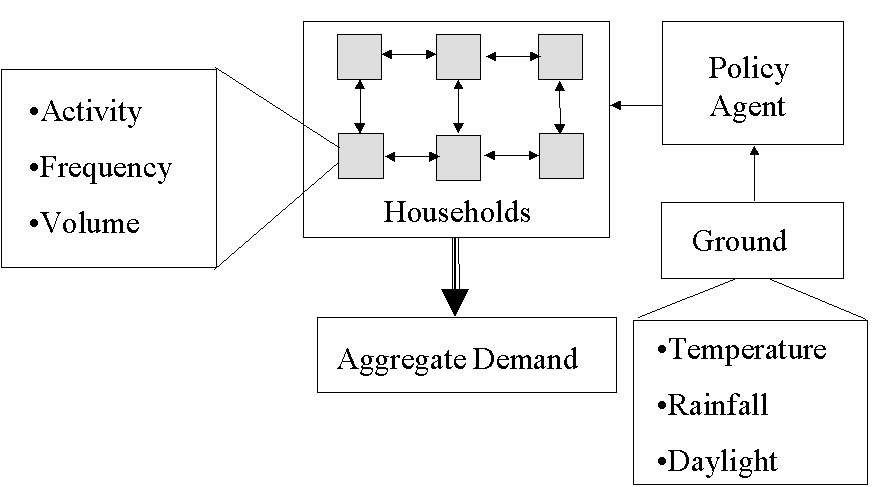
Figure 9. The structure of the water demand model
Households are influenced by their neighbours and the policy agent to different extents. The modeller decides what proportion of households are amenable to influence from these two sources (and hence those who are pretty much immune to influence). In fact all households can be influenced by these two sources but to widely differing extents. When deciding their water consumption they will take into account: what they have done before, what they did last time, what their neighbours have done, what the neighbour most similar to themselves has done, and what the policy agent is suggesting.
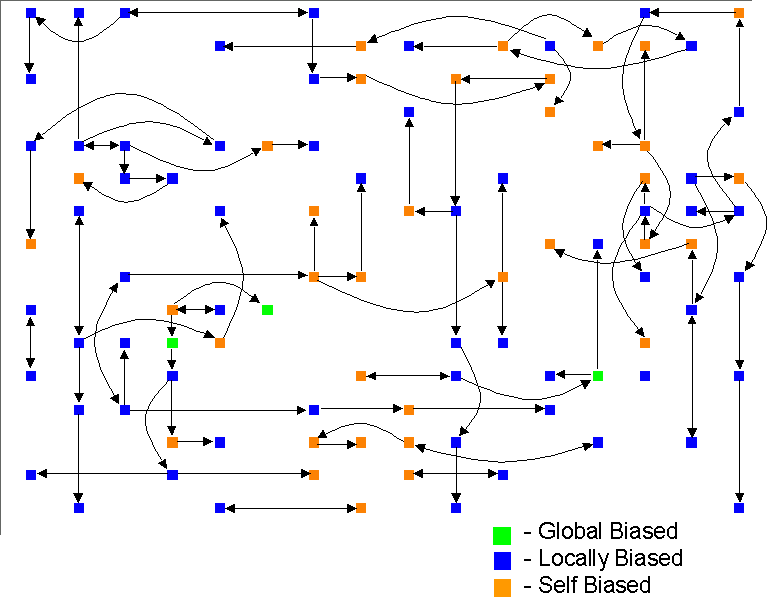
Figure 10. The pattern of most influential neighbour in an instance of the model (the arrow shows the direction of influence)
To give an idea of the sort of social network of influence that results, I have mapped out the influence due to the most influential neighbour only in Figure 10 above. To simplify the presentation I have labelled those that are most amenable to influence from neighbours as ‘locally biased’, those liable to be influenced by the policy agent as ‘globally biased’ and those not very amenable to outside influence as ‘self biased’.
Figure 11 shows an example set of results. This shows the aggregate demand patterns for 11 runs of the same model with the same parameters. However the positions of the household are randomly determined at the start of each run so that there will be a different network of influence and the exact appliances and initial patterns of use will be also freshly distributed at the start of each run (although in all cases so as to be consistent with the known distribution of such appliances and uses). Thus the different demand patterns that result are caused by these. The structure of the model allows for different experiments to be run, for example with different: climatological data; density of households; proportions of ‘locally biased’ households; or available appliances. In each case the results and the detail of the model can be run past experts and stakeholders for their critique as well as compared with known real demand patterns.
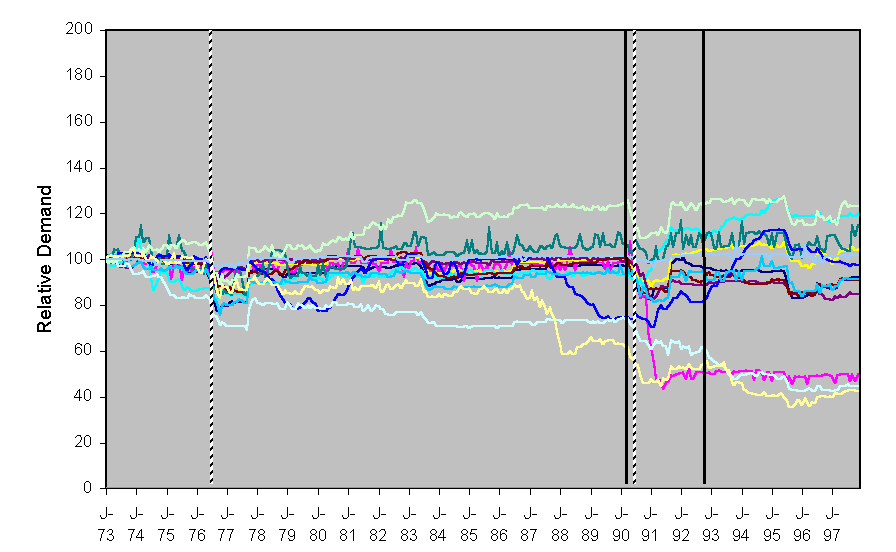
Figure 11. An example set of aggregated water demands (scaled so the demand is 100 at 1973) – each line results from a different run of the model with the same parameters. The dotted lines indicate the start of the major droughts, the solid lines indicate when new kinds of appliances became available.
As is evident in Figure 11, although there were some trends across all runs (for example by a temporary reduction in demand in response to a drought) there was considerable variation between runs. It seemed that localised patterns of behaviour could be self-reinforcing so that they were relatively immune from outside influence and robust against temporary effects. This was consistent with comparisons of patterns of consumption between different localities – different areas did have their own patterns of behaviour. These patterns did undergo some sharp and unpredictable changes in direction but they did have some common factors in response to common factors such as droughts.
What was learned as a result of this model? We certainly were not able to predict how domestic water demand would be affected by climate change. In fact the model helps demonstrate how the contingencies of neighbourhood interaction could significantly change the aggregate pattern of domestic water consumption. Thus it gave us reason to suppose that the actual pattern would not be easily predictable. It indicated that it was possible that that processes of mutual social influence could result in widely differing patterns of consumption that were self-reinforcing. More than this, the model provides a detailed and critiquable account of how this might occur. This lead to new questions about how households might be influenced and so, hopefully, to new attempts to discover the answers to these questions. Thus the model informed observation of the phenomena as it was informed by it. It also started a long process where by behavioural influences on water consumption are laid open to detailed criticism by experts and stakeholders so that the model may be improved. Thus it makes new sorts of hypotheses amenable to criticism and hence become a legitimate subject for scientific discourse.
Example 2: integrating domain expertise and aggregate data
The second model I will briefly discuss explicitly aims to integrate qualitative domain expertise expressed in terms meaningful to the practitioner and consistency with known time series. The purpose of this is to enable the exploration of possible consumer clusters that are otherwise difficult to obtain or estimate. This is described in greater detail in (Edmonds and Moss 2002).
To do this the modelling process has been staged, so that the more abstract parts of the model are specified first; and the more specific, context-dependent details last. There are three such ‘stages’.
This three part structure is illustrated in Figure 12. Within the generic framework there are many possible market contexts and within each market context there are many possible preference models.
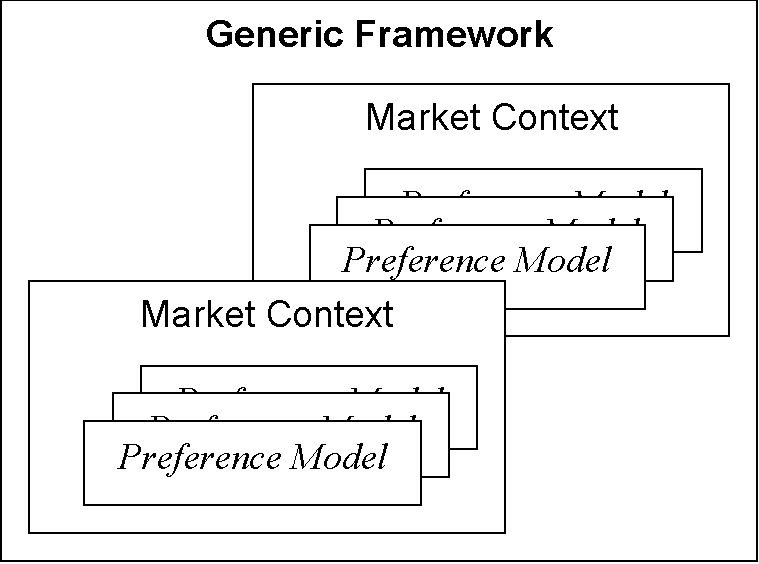
Figure 12. The three layers of specification
The three different layers gain their justification in different ways. A particular preference model is justified by how well it matches the aggregate time series as well as its credibility in the eyes of the practitioner. If a preference model is not satisfactory then another model needs to be tried. When the computer is searching for models it can go round this cycle very rapidly but can only judge models on its error with respect to the time series. The context is justified by the opinion of the practitioner and the success with which the search for preference models has gone. If no satisfactory preference models can be found then this brings into question the market context. The generic framework is justified on the success of the other two layers of model and the assumptions on which it is built. These assumptions are chosen from those generally accepted in the marketing literature of preference models and also so as to be as unrestrictive as possible. The fact that we are delaying a lot of the detailed specification to the practitioner allows us to avoid some of the more questionable assumptions. Of course, if a practitioner was not able to specify a reasonable market context in which a satisfactory preference models was identifiable then this would be evidence that the generic framework was either deficient in some way or had a more restricted range of applicability. Each layer is difficult to prove correct, but can be shown to incorrect (Popper 1968); the more abstract levels are less amenable to such falsification as it takes a lot of searching in the lower levels to effect this. The cycles of model developed at all levels is illustrated in Figure 13.
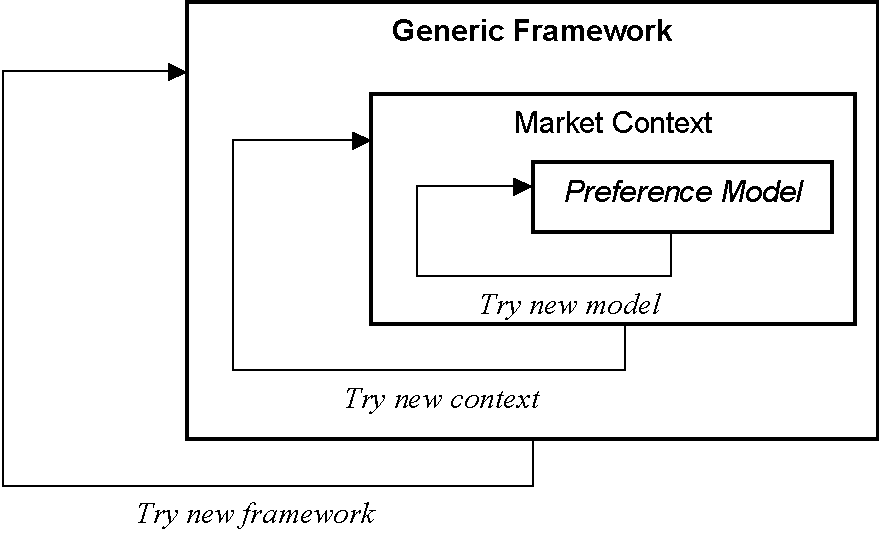
Figure 13. Three layers of development
Once the market context is specified, practitioners can explore the relation between a preference model and the aggregate data model in two different ways. They can specify a preference model and see what this model would mean when calculated with the price data. The resulting projections can then be compared with the aggregate sales data both in terms of the error and the pattern of the projected sales. Alternatively they can get the computer to search for and develop preference models within the market context that match the sales data. Here the market context has a second function: to restrict the vast range of possible preference models down to a more manageable sub-space of models – this makes the computation more feasible. The particular technique we used was adapted from those of Genetic Programming (Koza 1992, 1994), which allows for structure as well as the parameterisation of solutions to be induced. This sort of algorithm is good at finding acceptable novel solutions to relatively hard problems rather than finding the optimal solution to relatively easy problems. Thus the induction technique suggests possible models to the practitioner, it does not pretend to find the best or the true preference model. These possible ways that the preference models may be explored are illustrated in Figure 14.
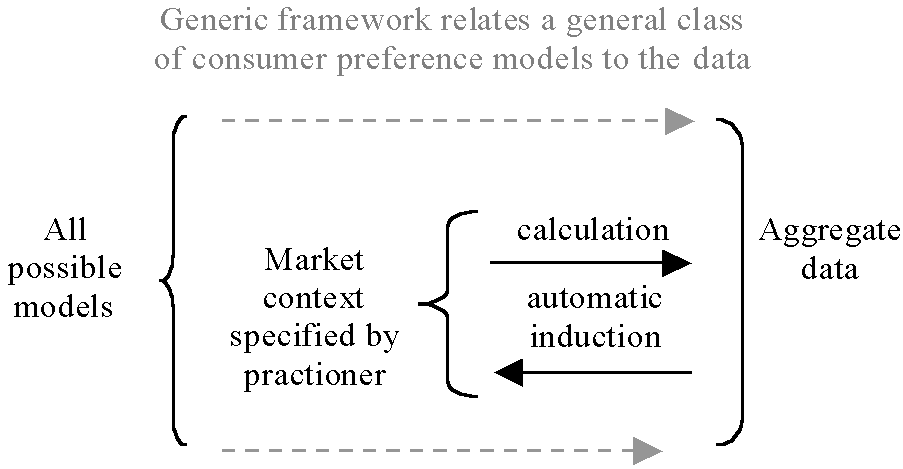
Figure 14. Exploring the relation between preference model and aggregate data within the market context and generic framework
A typical sequence of use is as follows.
The results can be presented as follows. These are taken from an application to the UK market for liquor. Here we had aggregate price and sales data for 96 weeks, for 4 brands at each of two bottle sizes. The characteristics that were specified by the practitioner were: relative price, size, expansiveness, ‘specialness’ and ‘uniqueness’. Relative price was calculated from weekly data, expansiveness was calculated as the long-term average of the raw price, size came from the brand data, specialness and uniqueness were estimated by the practitioner on a Likhert scale for each brand. One brand in the smaller size was selected as the focus brand. Three of the brand/sizes were selected as not competitively interacting with the focus brand which left 5 brand/size combinations.
The characteristics of the best preference model found by the algorithm are summarised in Table 1. This model consisted of three clusters accounting for 21%, 49% and 29% of the purchases (called A, B and C, respectively). These clusters can be interpreted as follows: a low price and large size were important to the biggest cluster (B); the smallest cluster (A) prefers a relative expensive drink (although at a cheap price if they can get it) but not unique (i.e. not different from others – a well known and accepted brand); the final cluster (C) was less clearly defined but would prefer and expensive and unique drink and was more tolerant to a slightly higher price.
|
Cluster |
Relative Price |
Expansiveness |
Size |
Specialness |
Uniqueness |
|
A |
1 |
7 |
6 |
0 |
|
|
B |
1 |
5 |
8 |
5 |
|
|
C |
2 |
9 |
3 |
9 |
Table 1. A summary of a consumer preference model. The numbers represent the ideal value of product for that cluster (10=maximum, 0=minimum). Bold numbers indicate characteristics that were particularly important to the cluster. Those which were not significant to the cluster are omitted.
The marketing practitioner who we were working well immediately interpreted these as follows: Group A were ‘social drinkers’ buying bottles for a party or similar; B are the ‘functional drinkers’ who wanted the drink for the alcohol alone and C were those who were buying a bottle as a self reward. Regardless of whether this was an accurate interpretation or not it illustrates how the preference model was readily interpretable in terms that were meaningful to the practitioner. This was not just a shallow reading of the labels because this practitioner had ‘played’ with the system for quite a bit and had got the feel of what it could and could not do – the model had, to some extent, gained meaning from its use in practice inside a context that was familiar to the practitioner. This model also fitted the aggregate data well. Figure 15 shows the actual and projected sales figures for this preference model. The model was searched for (and hence ‘fitted’) to only the first 21 weeks of data, but shows a good level of fit over the rest of the data up to about week 75-80 after which it diverges. When the practitioner was asked whether anything had occurred to change the market around this time it was reported that a particular marketing campaign was launched.
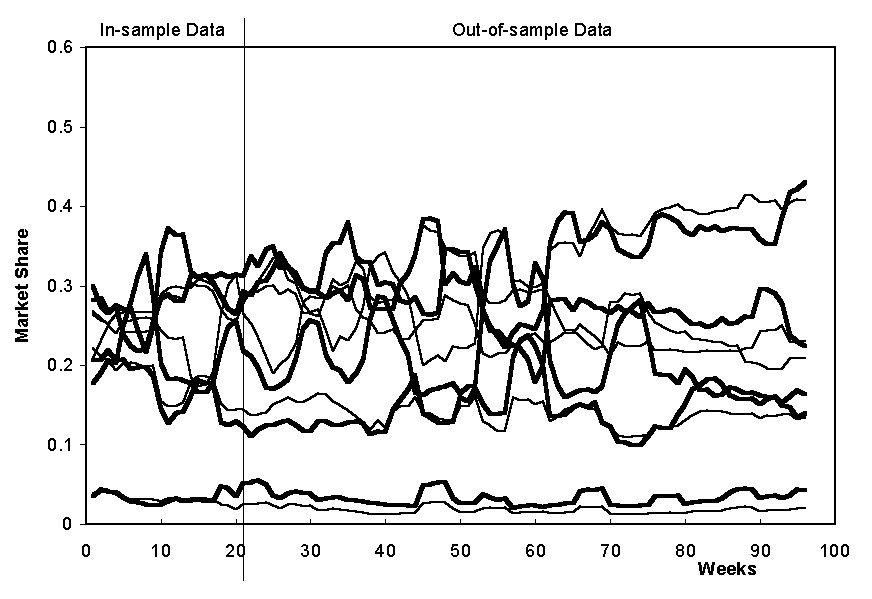
Figure 15. The aggregate sales data (real data for the 5 brands is displayed as bold lines and the projected sales as thin lines)
Conclusions
To conclude I will list some of the dangers from the misuse of simulation models and then list some of their possible (positive) uses.
The principle dangers seem to be the unintended deception of self and others as to the justification of models and the interpretation of the results. A confusion between explanatory and predictive types of model seems to occur often – I am particularly aware of this occurring in economics where models will often be constructed as if they were predictive, so that their mechanisms do not necessarily correspond with the phenomena (thus ruling out good explanations), but the models are validated as explanatory models using a system of in-sample and out-of-sample data instead of against data unknown to the modeller. When a set of such models was tested against new data (produced after publication and hence unknown to the modellers), almost all of them failed (Mayer 1975).
A second confusion is where an intermediate conceptual model is being simulated but the results are projected directly upon the target phenomena. Here the semantic aspect of the model are being confused with a more direct relationship against data models of the phenomena. An example of this is in (Axelrod 1984), where after investigating an abstract model justified entirely on conceptual terms Axelrod claims general conclusions about when cooperation based on reciprocity can evolve:
"In this chapter Darwin’s emphasis on individual advancement has been formalised in terms of game theory. This formulation establishes conditions under which cooperation based on reciprocity can evolve." (end of Chapter 5)
A final confusion I will highlight is that of confusing descriptive models and generative models. A descriptive model is simply a way of characterising or portraying the results, it does not say anything about how those results were produced. A generative model relates to the way the target phenomena are generated. For example, a particular data-generating process may not have a defined finite variance, although any finite set of data from this process will have a variance that you can calculate. In this case one could describe the data with a standard probability distribution but it would be a mistake to suggest that the data was generated from such a distribution.
However these danger do not mean that simulation modelling should be avoided. So I finish by suggesting some sound uses for simulation models. The most mundane use to as a ‘second best’’ option when analytic solutions are not possible – simulation allows the exploration of very complex models. A more interesting use is to establish possible processes and outcomes – this can be particularly useful for establishing counter-examples to assumptions in other models. A simulation model can also be very useful as part of a dialogue with domain experts and stakeholders as a way of informing good observation of phenomena by revealing assumptions and helping to frame important questions. Finally simulation models can be used as computational descriptions of phenomena which may then be further abstracted into more general models – then when a question about the detail of the general model arises the justification for that can be traced back in terms of the working of the simulation model.
Thus my conclusion is that, as with any other tool, simulation modelling can be very useful but you have to think about how you use it. To use it well takes just as much skill and care as for using, for example, mathematics. Simulation can be used in areas where it is difficult to make useful analytic models of, and has other advantages as well. It also has its own particular sets of pitfalls and dangers. There are no magic shortcuts to understanding complex phenomena, so we need to apply the full range of available tools in order to gain what progress we can.
Acknowledgements
Many thanks to Valerie Feldmann and Katrin Muehlfeld for inviting me to their workshop on "Virtual Worlds of Precision - Computer-based Simulations in the Natural and Social Sciences" at Oxford in January 2003 and for the workshop participants for their interest and questions during the event. Also, as ever, thanks to Scott Moss for many discussions about the above matters, even if he does take a while for him to see that I am right. The water demand model was financed by the Department for Environment, Fisheries and Agriculture in the UK as part of the CC:DeW project and also as part of the EU 5th framework project FIRMA (Freshwater Itengrated Resource Management with Agents). The system for integrating marketing domain expertise and aggregate data was developed in the IMIS (Intelligent Marketting Integrated System) project with funding from the Department of Trade and Industry and the Engineering and Physical Sciences Research Council in the UK. Thanks to Clive Sims his advice and feedback of the development of IMIS.
References
Axelrod, R. (1984) The Evolution of Cooperation. New York: Basic Books.
Axtell, R. L. and J. M. Epstein (1994). Agent-based Modelling: Understanding our Creations. The Bulletin of the Santa Fe Institute 9:28-32.
Bennett, C. H. (1988). Logical Depth and Physical Complexity. In The Universal Turing Machine, A Half-Century Survey. Oxford, Oxford University Press: 227-57.
Cartwright, N. (1983). How the Laws of Physics Lie. Oxford, Clarendon Pres.
Clancey, W. J. (1997). Situated Cognition: On Human Knowledge and Computer Representations. New York: Cambridge University Press.
Davies, G. M. and Thomson, D. M. (eds.) (1988) Memory in context: context in memory. Chichester: Wiley.
Downing, T. E, Butterfield, R. E., Edmonds, B., Knox, J. W., Moss, S., Piper, B. S. and Weatherhead, E. K. (and the CCDeW project team) (2003). Climate Change and the Demand for Water, Research Report, Stockholm Environment Institute Oxford Office, Oxford.
Edmonds, B. (1999a). Pragmatic Holism. Foundations of Science 4: 57-82.
Edmonds, B. (1999b). Syntactic Measures of Complexity. Doctoral Thesis, University of Manchester, Manchester, UK. (http://bruce.edmonds.name/thesis/)
Edmonds, B. (1999c). The Pragmatic Roots of Context. In Bouquet, P. et al. (Eds.), Modeling and Using Context: the Proceedings of CONTEXT'99, Trento, Italy, September 1999. Lecture Notes in Artificial Intelligence, 1688:119-132.
Edmonds, B. (2000). The Use of Models - making MABS actually work. In. S. Moss and P. Davidsson. Multi Agent Based Simulation. Berlin, Springer-Verlag. Lecture Notes in Artificial Intelligence 1979: 15-3.
Edmonds, B. (2002) Simplicity is Not Truth-Indicative. CPM Report 02-00, MMU, 2002 (http://cfpm.org/cpmrep99.html).
Edmonds, B. and Moss, S. (2002) Integrating Domain Expertise With Aggregate Data Using Evolutionary Computation. CPM Report 02-97, MMU, 2002. (http://cfpm.org/cpmrep97.html).
Feyerabend, Paul K. (1975) Against method: outline of an anarchistic theory of knowledge. London: NLB.
Giere R., N. (1988). Explaining science: a cognitive approach. Chicago ; London, University of Chicago Press.
Gunsteren, W. F; Berendsen, H. J. C. (1990) Computational Simulation of Molecular Dynamics: Methodology, Applications and Perspectives in Chemistry. Angewandte Chemie - International Edition in English, 29:992-1023.
Hesse, M. B. (1963). Models and Analogies in Science. London, Sheed and Ward.
Hughes, R. G. (1997). Models and Representation. Philosophy of Science 64 (proc): S325-S336.
Koza, J. R. 1992. Genetic Programming: On the Programming of Computers by Means of Natural Selection. Cambridge, MA: MIT Press.
Koza, J. R. 1994. Genetic Programming II: automatic discovery of reusable programs. Cambridge, MA: MIT Press.
Kuhn, T. S. (1962). The Structure of Scientific Revolutions. Chicago: University of Chicago Press.
Mayer, T. (1975) Selecting Economic Hypotheses by Goodness of Fit. The Economic Journal 85:877-883.
Morgan, M; Morrison, M (eds.) (1999). Models as Mediators: perspectives on natural and social science. Cambridge: CUP,
Popper, K. (1968), The Logic of Scientific Discovery, Hutchinson, London.
Rosen, R. (1978). Fundamentals of measurement and representation of natural systems. New York, North-Holland.
Suchman, L. A. (1987). Plans and Situated Action. New York: Cambridge University Press.
Suppes, P. (1962) Models of Data. In Nagel, E; Suppes, P; Tarski, A (eds.). Logic Methodology and the Philosophy of Science: Proceedings of the 1960 International Congress. Stanford, CA: Stanford University Press, 252-261.