The popular admonition to "Keep It Simple Stupid" or KISS, makes good sense if you are designing or constructing something – that is, if one has a particular specification, function or purpose in mind and one is trying to construct something appropriate. In this context the advice makes sense in two ways: firstly, that the more complex something is the less easy it is to control (and hence to make it do what one wants); and, secondly, in circumstances where a particular design does not work that one should resist elaborating it in an attempt to make it work but rather one should engage in a more fundamental re-evaluation (since such elaboration seldom really works) [7].

However the KISS sentiment is often also applied to the business of modelling some phenomena, e.g. with a simulation or a set of equations. So that even when faced with obviously complex phenomena modellers strive to keep their models simple, to an extent that is beyond any evident justification. The reasons for this are varied, if often left implicit. There are obvious practical reasons for keeping a model simple – this makes it easier to: implement; manipulate; analyse; check; communicate, etc.. However, it is sometimes claimed (and often implied) that the advantages of simplicity go beyond these practical values – that a simpler model is more likely to be true; or gets closer to the essence of the matter. In other words, that a simpler model is, in general, fundamentally better – it is this we are arguing against.

We suggest a new slogan: "Keep It Descriptive Stupid" or KIDS – which is supposed to suggest the approach to modelling where one starts with a descriptive model (which may be quite complex) and then only simplifies it where this turns out to be justified. This is in contrast to the KISS paradigm where one only tries a more complex model if simpler ones turn out to be inadequate. Multi-agent based simulation (MABS) not only facilitates the KIDS approach but epitomises it. Thus the importance of the move towards MABS can be seen as part of a broader movement away from unjustified abstraction in modelling – abstraction that is, since the advent of accessible computational power, frequently unnecessary.

We necessarily can not deal with all the issues this paper raises – this would take a book rather than a workshop paper. Thus this paper has to be more in the way of a summary which passes over many of the arguments. We are forced to refer to our previous work for many of these issues – these will provide a more adequate entrance to the relevant literatures. We apologise for this. Thus for more on the meaning and definition of complexity see [6]; for the issue of how and why one might judge one model to be better that another see [9, 11]; for more on the relation of the scientific process to simplicity see [7]; for an extended paper on why simplicity is not truth-indicative see [10]; for more on the relation of formal systems to the scientific process see [8]; for more on the intended theory/implemented simulation distinction and its ramification see [9, 14]; and for more on constructive ways forward see [11].

We are limited beings, which could explain why simplicity has such advantages and attractions for us. It also seems we have a tendency to project our own characteristics upon the natural world, thus we would like to think that everything has an "inner" simplicity even if they appear to be very complicated. Sometimes this is expressed as an assumption that simplicity is a (fallible) guide to truth, sometimes by conflating simplicity with generality (hiding the assumption that simpler models will apply to a greater variety of real cases, an assumption that is often unjustified).

When a modelling decision is justified using a phrase like "for the sake of simplicity" it is implicit that this is (in some sense) a good justification. People do not tend to justify their modelling decisions in papers using phrases such as: "it would have taken too long"; "we could not think how to do this"; or "it would make it very hard to check", despite the fact that, in our view, these are perfectly acceptable (indeed inevitable) reasons for beings with limited resources (like us). Rather, often it seems that people invoke simplicity because of its positive connotations, even if it was the more practical reasons that motivated them (of course, they also do so because that is what they were taught, but presumably the teachers had some reason for supposing this etc.). Thus the philosophical tradition that somehow simplicity is truth indicative gives credence to modelling decisions that are not otherwise explicitly justified. Elsewhere I (BE) argue that simplicity is not truth-indicative [10].

Rather we suggest that one would expect that, for many purposes and for many phenomena, that the models will need to be complex if they are to be adequate for the purposes for which the model is built. Given that much that we study is complex, it would be very surprising if it always turned out to be the case that the models could be simple. Surely the burden of proof is on those who insist that it is not sensible to try and match the complexity of the model with the complexity of the phenomena being modelled. The facts that complex outcomes can emerge from apparently simple systems (as in mathematics or ALife) does not mean that the complex phenomena we now observe is reducible to simple models. Even if (a huge presumption) a certain phenomena was generated using simple mechanisms, this does not mean the results we observe now are simple or could be usefully represented with a simple model. For more on the difference between kinds of complexity see [6].

To make this clear consider an analogy with a 19^th Centaury naturalist making sketches of animals. The naturalist is doing this in order to help correctly identify and classify new species. It would have been laughable to suggest that such sketches should be limited to line cartoons "for the sake of simplicity", "so that they have the greatest possible generality", because the different species would not have been identified yet. It may have been that small details would have turned out to be important later for distinguishing closely-related species. Only when the naturalist had examined (and sketched) enough individuals would it have become clear which details were relevant and which not. The details that turned out to be essential may have allowed the drawings to be significantly simplified a posterior, but in many cases only marginally simplified (as with moths). The point is that it is simply not appropriate to make simplifications before one knows what is relevant and what is not. Simply hoping that one may have chanced upon an appropriate simplification does not make that simplification justified.

This is even more evident when one is considering the domain of interacting systems of flexible and autonomous actors or agents. The relevant behaviour of many such systems will not be simple, in particular they will not be reducible to aggregate models (for example statistical models) without significantly diverging from their target systems (that is, the agents are ‘embedded’ in their society in the sense of [17]). This includes multi-agent systems that are designed for a specific purpose [12]. Adopting a multi-agent model represents a move towards descriptive accuracy since: actors or agents in the target domain are represented by agents in the model and communications by messages between the agents. That is MABS allows and facilitates a more direct correspondence between what is observed and what is modelled. One benefit of this move to descriptive MABS is that a whole swath of evidence becomes available for validating our models – straight-forward descriptive evidence gained from observation of the domain can be applied to the model by virtue of the more straight-forward correspondence. What is new is that this evidence may be anecdotal or "common-sense". Previously such evidence may have been rejected on the ground that it is not "scientific" or "rigorous", but this was because it was not formalisable in terms of the current modelling technology (analytic mathematics) and hence had no deducible outcomes that could be checked. Now such qualitative information can be formally modelled in simulations where the deduction of outcomes is performed computationally rather than analytically. Further, in a descriptive MABS, this is relatively easy and natural and combines naturally with participative approaches to model construction and validation, as in [2].

Given that such evidence can be made rigorous and thus brought within the domain of the scientific, it should not be ignored. Thus if you have a target domain in which there is such evidence (such as "it seems that the actors learn to avoid areas where they were mugged") then models should only ignore such evidence if either: (1) there is good reason to think this is irrelevant or (2) there is evidence that this is wrong (e.g. over-simplified to the extent that it is significantly erroneous). In particular if one has access to a direct or expert "common-sense" account of a particular social or other agent-based system, then one needs to justify a model that ignores this solely on a priori grounds. In other words, constructing a model that is simpler only "for the sake of simplicity" may be a case of wilfully ignoring evidence.

Thus a move towards descriptive models allows for more of the available evidence to be applied. Of course, all available evidence should be used, including evidence that is traditionally used: time series data, point measurements, statistics etc. and evidence resulting from new methods of data collection (as suggested in [4]). This can be used as a sort of check of the anecdotal evidence, because one can check that a model constructed on the basis of anecdotal evidence is consistent with them (see [20] or references above for many others who suggest this). As with all data, one takes into account its reliability. Anecdotal evidence can be unreliable – however this does not mean we should not use it, merely that we need to cross-check it (as with any other useful but fallible evidence), but this is exactly what MABS facilitates.

This is an uncomfortable lesson for us: that the common-sense description may be a far better starting place than an artificially simple construction based on the guesses of academics. However, if one is modelling social or multi-agent systems, where the phenomena is undoubtedly complex (making a priori guessing difficult) it is not sensible to ignore any evidence that may help us. The more complex the phenomena the more evidence as to its workings are needed.

One common response to the arguments above is to claim that one is doing a sort of applicable mathematics rather than science. That is, one is not claiming that a particular model (or simulation) represents in any sense any observed phenomena but that one is merely establishing the model’s properties, so that in the future someone may be able to successfully apply it to solving real problems. I call this the "formalist stance" – it is often adopted in fields which are currently lacking significant empirical or practical success (e.g. AI or Economics). The argument goes thus: much mathematics that was driven by goals other than representing reality (but sometimes including simplicity) turned out to be very useful later on, might not the same thing happen with developing abstract simulations. The answer is that this is possible, but then the simulation (or model) should be judged by the same sort of criteria as is used to judge new mathematics, namely: precision, soundness, importance and generality. The assumptions/mechanisms upon which the results depend should have been made completely explicit and precise. The model should be very thoroughly tested to almost eliminate any possibility of error in the results (this will almost certainly involve a wide search of the parameter space and independent replication in the case of complex simulations). The results should be sufficiently important in that they effectively present (to us humans) new information about the system that is not available from a casual inspection of the simulation set-up and inputs. Finally, it should be established that the results are applicable to a wide range of kinds of system. All too often simulations that are claim protection under the formalist stance do not justify themselves against these criteria but rather via the credibility of their results in terms of observed phenomena. Thus they fail to satisfy any set of relevant academic criteria. These issues are discussed further in [8].

To summarise, the KISS approach says that one needs a good reason not to use the simplest model, and then allows for progressively more complex models if simpler ones turn out to be inadequate. In contrast the KIDS approach starts with a model that is as straight-forwardly descriptive as evidence and resources allow (even if this means that one starts with relatively complex model) and then allows for progressive development later (including simplification and abstraction) as evidence and understanding of the model support this (it may turn out that some features that turn out to be important later have been left out, leading to an even more complex model). This is shown in Fig. 1.

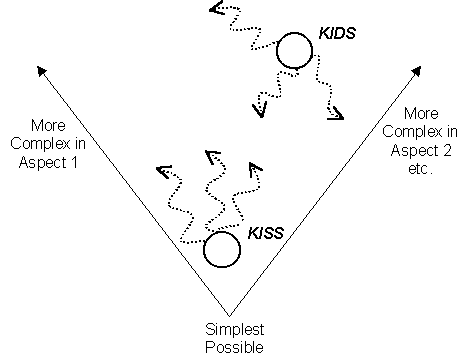
Fig. 1. An Illustration of KISS and KIDS

In this discussion it is important to distinguish between the intended theory and the implemented simulation (or model) that is meant to realise that theory in computational (or analytic) form. There are many ways in which this distinction is significant. In general, there will be many ways of constructing a simulation to embody any particular theory, because only certain aspects of the simulation are considered significant in terms of the theory, the rest being considered as the mechanisms to produce these. There will be various artefacts introduced as a side-effect of a particular implementation, so that the implemented model differs from the intended theory. This might be in ways that are considered unimportant, for example in miniscule deviations due to the pseudo-random number generator, or it may turn out to be significant (when a seemingly-innocent implementation detail significantly changes the results, e.g. as documents in [21]). All too often the implemented simulation and the intended theory are conflated or the intended theory is not described explicitly. This distinction is discussed further in [13].

In this paper we are arguing that the intended theory should (as a starting point) be as descriptive as possible and that a (single) simulation should be as direct a representation of this theory as is feasible. Of course, if there are two completely adequate ways of implementing the same theory as simulations then (for practical reasons) it is sensible to choose the simpler one. However feasibility considerations concerning the implemented simulation should not lead one to simplify the intended theory – this would be a case of "the tail wagging the dog". Rather if it is infeasible (for whatever reason) to implement a simulation of the intended theory, then this should be explicitly acknowledged.

When it is infeasible to implement a simulation that is adequate (for a specific purpose) to the intended theory (a common case in social simulation) one has a number of ways in which one can proceed. Often the wisest course is to abandon formal (including computational) modelling as (at least currently) beyond our capabilities. This may be followed by a decision to change the modelling goal to something less ambitious – for example to restrict the theory to cover a small aspect or special case. This might result in a new intended theory that is feasible to implement. The temptation here is to not admit one has taken this step – to pretend (to oneself) that the resulting feasible simulation is somehow still a model of the original intended theory.

In this section we briefly outline a suggestion as to a constructive way forward in the face of extremely complex phenomena (such as with social systems and ‘non-toy’ MAS). More about this can be found in [11].

Before we even get to descriptive simulations one has a series of "Data Models" [23] – that is, descriptions or data obtained by either measurement or elicitation. These provide the foundations upon which descriptive simulations will be built.

When one has a number of descriptive simulations concerning a related class of phenomena (satisfying similar purposes), one may be in a position to see what is relevant to a more abstract simulation, by examining the processes that result in these. It may well be that the abstract simulation only applies to the behaviour of descriptive simulations under certain conditions or (to use terminology from physics) within certain phases.

It may then be possible to formulate analytic models about the behaviour of aspects of the abstract simulation. For example, it may be observed that a certain process dominates the results in certain conditions and this can be approximated by some analytic or statistical models. The huge advantage of approaching abstract and analytic models in this way is that it provides a traceable chain of reference to observations of the phenomena. Thus if we ask why a certain term has a particular exponent in an analytic model, we can point to the behaviour in the abstract simulation this approximates. This can guide us when adapting or improving the analytics, especially when we are fault finding. Similarly, the mechanisms in the abstract model can be traced to the descriptive models it represents etc.

If one is in the fortunate position where a number of these analytic models or abstract simulations concur then this might be a sought-after general theory covering a range of phenomena. Such a theory can then be tested against the class of phenomena it concerns.

Later on, once the general theory has been thoroughly validated in multiple ways, it may be possible to simplify and systematise it. This process has occurred frequently in Physics. Whereas only a few people could understand Newtonian mechanics as it was first presented, nowadays it has been systematised into the accounts found in standard school text books. Such systemisation and simplification greatly facilities its applications to problems and new phenomena.

It is highly unlikely that ‘short-cuts’ to the simple or general theories will be discovered without a substantial amount of lower level data-collection and modelling has occurred first. This seems to be because the human mind requires conceptual frameworks to work within, which then trap us into formulating models similar to those that have gone before. It often seems to require a substantial (if sometimes indirect) ‘jolt’ from the phenomena itself to guide us towards really useful theory.

To summarise this, complex phenomena will not only require more complex simulations, but also the development and maintenance of complex clusters of models, as suggested in [16]. There are other ways in which such clusters may be created, such a using a number of models in parallel to cover different aspects of the same intended theory, this is discussed to a limited extent in [11].

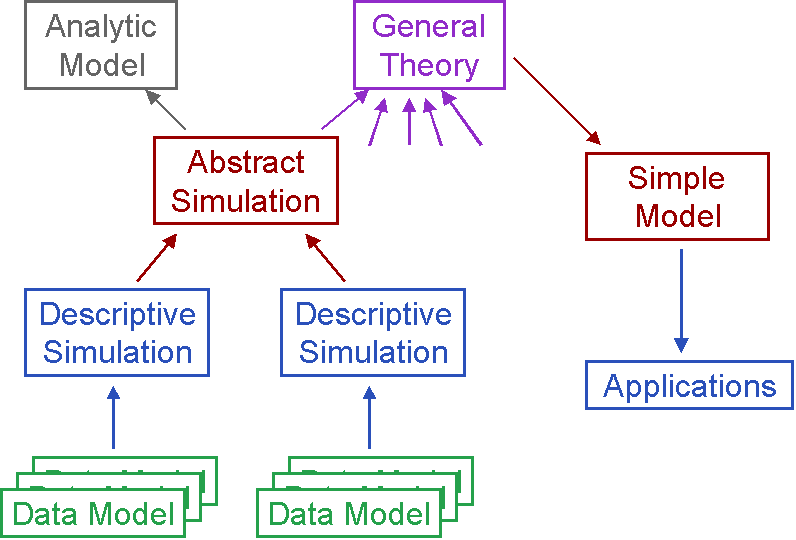
Fig. 2. An illustration of the bottom-up way of model development

The purpose of this section is to illustrate the KISS approach. Thus we have here started with a model that encapsulates the aspects of the target domain for which we have (formal or informal) information. We then explore the behaviour of the model when different aspects stay the same – that is to see if one can find any aspects which do not have a relevant and significant impact on the chosen outcomes. This would then suggest a hypothesis that a simpler model is possible, which excludes this aspect. If all aspects seem to be essential to maintaining the properties of the outcomes that are deemed to be representative of what is reported, then this suggests that a simpler model would not be descriptively adequate. If this is the case it is difficult to see that such a model would have been reached by starting from a simpler model and elaborating it. Of course what we have is a complex model whose behaviour is not fully understood – it acts as an intermediary between observation and theory building.

The model in this example is a descriptive social simulation. It seeks to see how the patterns of domestic water demand in localities may be explained by mutual influence. To be exact, it models how a set of stakeholders perceived that households might interact because it was developed as the result of some input from a panel of representatives from UK water companies and other domain experts. This model aimed to: capture their qualitative informal suggestions (e.g. demand rebounds fairly fast after a drought); be consistent with known data about households (e.g. ownership/frequency/use data); and have aggregate demand patterns similar to those observed (e.g. with clustered volatility). It was developed as part of the FIRMA and CC:DEW projects – for a more detailed description see [5]. The initial model was written by Scott Moss and then developed by Olivier Bathelemy and Bruce Edmonds.

The core of this model is a set of agents, each representing a household, which are situated on a grid. Each of these households is allocated a set of water-using devices in a similar distribution to those in the mid-Thames region of the UK. At the beginning of each month each household sets the frequency the appliance is used (and in some cases the volume at each use, depending on the appliance). Households are influenced as to their usage of these appliances by several sources: their neighbours and particularly the neighbour most similar to themselves (for publicly observable appliances); the policy agent; what they themselves did in the past; and occasionally the new kinds appliances that are available (in this case power showers, or water-saving washing machines). The individual household’s demands are summed to give the aggregate demand. Each month the ground water saturation is calculated based on weather data (which is past data or past simulated data), if this is less than a critical amount for more than a month, this triggers the policy agent to suggest a lower usage of water. If a period of drought continues it progressively suggests using less and less water. The households are biased to attend to the influence of neighbours or the policy agent to different extents – the proportion of these biases are set by the simulator. This structure is illustrated in Fig. 2.

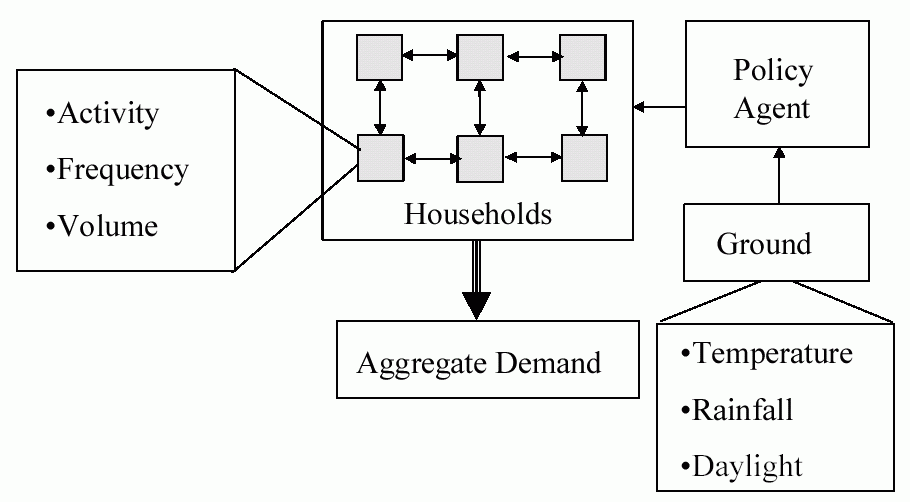
Fig. 3. The structure of the water demand model

The neighbours in this model are those either those in the shape of a cross or a square neighbourhood (Fig. 3). The extent of this neighbourhood is parameterised by the area (in the cases in Fig. 3 this is 8).

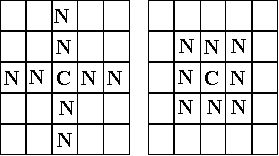
Fig. 4. The neighbourhood pattern for the households, left cross, right square (each area 8)

Every neighbour has a unique most neighbour who is most influential to it, the topology of this social network consists of a few pairs of mutually most influential neighbours and a tree of influence spreading out from these. The extent of the influence that is transmitted over any particular path of this network will depend upon the extent each node in the path is biased towards being influenced by neighbours.

Households are also (to a lesser extent) also influenced by all its neighbours in its neighbourhood. The edges of this may or may not be wrapped around into a torus. The focus model used an unwrapped cross-shaped neighbourhood so the households at the edges and corners have fewer neighbours that those in the middle. The reason for this that the resulting patterns seem to us a reasonable mix of locality and complexity (data on the actual patterns was not available).

In each run the households are distributed and initialised randomly, whilst the overall distribution of the ownership and usages of appliances by the households and the biases of the households is approximately the same. In the runs described herein the same weather data is used, so the timing of droughts (and hence advice from the policy agent) and of new innovations are the same in each run.

The graphs below (such as Fig. 4 immediately below) show the aggregate demand resulting from many runs of the same set-up (rescaled so that 1973=100 for ease of comparison). Each line shows a different run from using that set-up, so you can see the variations in aggregate behaviour possible from the same model. Significant events include the droughts of 1976 and 1990, which often show up in a (temporarily) reduced water demand, due to agents taking the advice from the policy agent to use less water. Power showers become available in early 1988 and water-saving washing machines in late 1992 which can cause a sudden increase or decrease respectively.

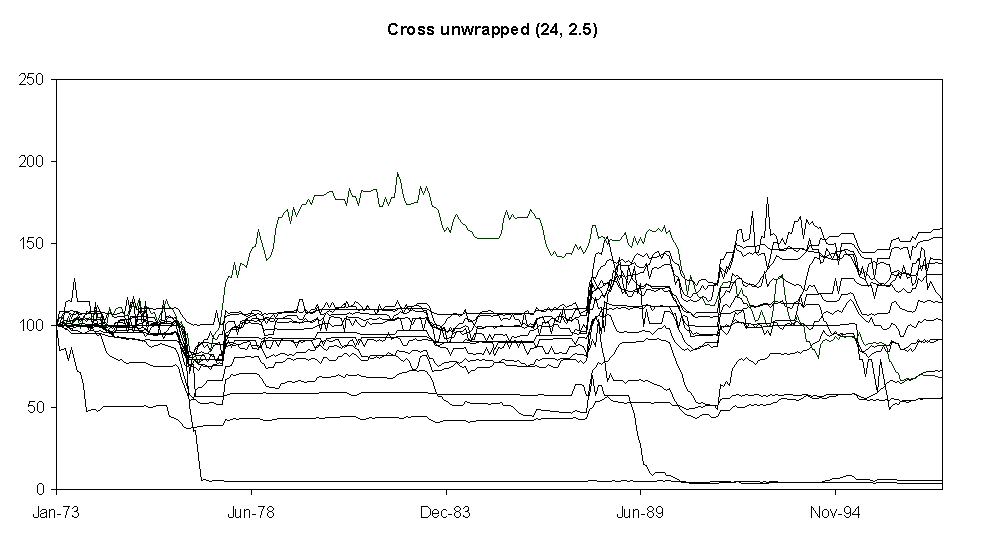
Fig. 5. Relative aggregate demand levels (cross-shaped unwrapped neighbourhoods of size 24)

Fig. 4 shows the model set-up chosen as the starting point for the model variations. It shows 15 different runs of that model. The droughts of 1976 and 1990 are clear as dips in demand in most (but not all) of the runs and the introduction of power showers in 1988 precipitate a sharp upturn in demand. It is noticeable that each such ‘shock’ can cause a lasting period of volatility in a demand line, possibly in the opposite direction as the original shock (as in the top line in Fig. 4). This seems to be because the influence is not significantly dampened but ‘rings’ around the model and changes become locked-in due to mutually self-reinforcing influence between households. Fig. 5 shows the difference when the network of influence is limited to only adjoining neighbours which cuts out most of the social influence. The pattern is usually regular and predictable for most households –unlike observed patterns of water demand.

It is important that each run can turn out to be different, even though the parameters and set-up is the same. This is due to the fact that, in the Thames Valley in the UK, very similar neighbourhoods (in terms of socio-economic profile and size) can display very different patterns of aggregate water demand. Thus this model is not only intended to capture a typical water demand response but the range of water demand responses. For this reason one run (or even statistics about many runs) is insufficient to characterise the output from a particular model set-up. Thus in the examples below we will show a set of runs, to give some idea about the range of behaviours that each set-up can exhibit.

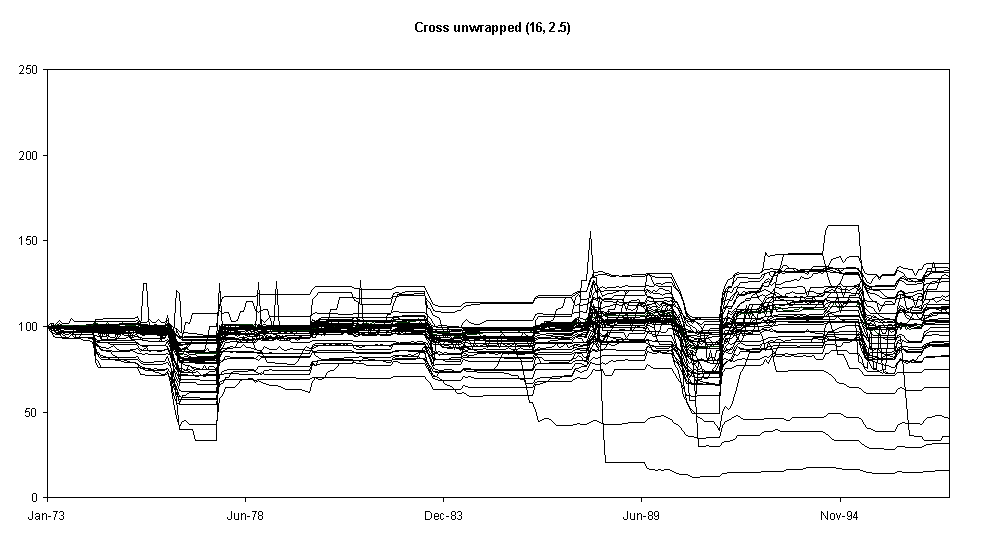
Fig. 6. As Fig. 4 but with neighbourhoods of size 4

Next we change the topology of the social influence network so that the social relations are wrapped-around as if they lived on a torus – this is shown in Fig. 6. This has the effect of increasing the short-term volatility of many of the runs but decreasing the longer-term variation in a run. It seems that the whole population can ‘flip’ from one behaviour to another – they are too connected. This contrasts with the runs shown in Fig. 4 where different behavioural ‘regimes’ may be found on different edges of the population. The shape of the neighbourhood also seems to make a difference.

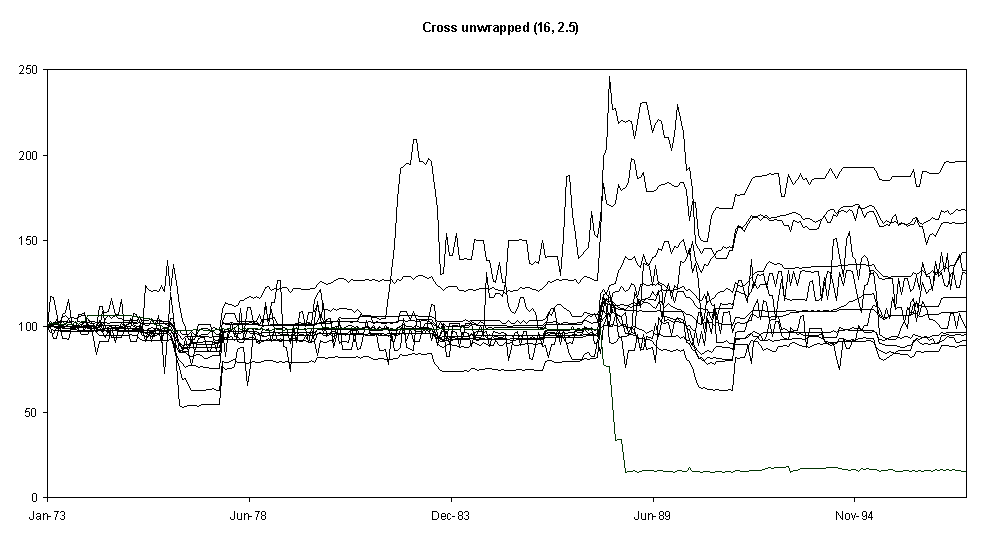
Fig. 7. As Fig. 4 but with wrapped neighbourhoods (rather than unwrapped)

Fig. 7 shows the what happens when the shape of the neighbourhood is changed to a block shape (see Fig. 3). This appears to lessen the impact of droughts.

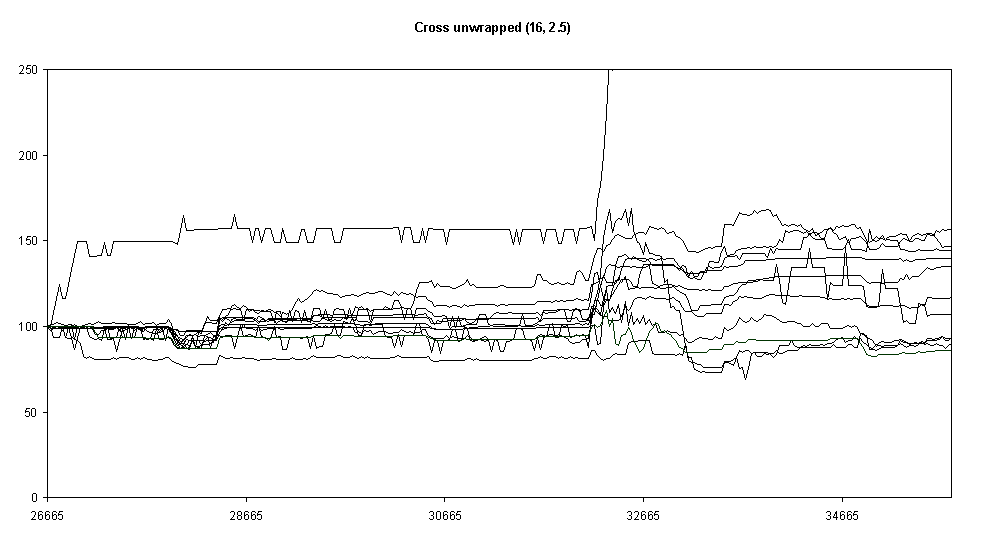
Fig. 8. As Fig. 4 but with block-shaped neighbourhoods (rather than cross-shaped)

Lastly we experimented with the memory coefficient. This halved the rate at which past behaviours are forgotten, this is shown in Fig. 8.

Fig. 9. As Fig. 4 but with a memory coefficient of 5 (rather than 2.5)

Unsurprisingly many of the lines are a lot flatter. In particular many more of the demand patterns reverted after droughts to the levels they were before them. The introduction of innovations still has an affect on the general levels.

Elsewhere [3] it was shown that the: climatologically data: the timing of innovation introduction; and the proportion of different biases as to influence sources can all make a marked qualitative difference to the aggregate demand patterns that result. However [3] also showed that the shape of the initial distribution of the use of appliances in households turned out not to be important and hence could be simplified. Thus this element is a candidate for simplification.

To summarise these results and those from [3]. it appears that the following elements of the model are important to the kinds of results that one gets out of the model: the number and size of droughts, the distribution of biases of the households, the timing of innovations, the rate of forgetting, the neighbourhood shape, the topology of the influence grid, and the size of the neighbourhoods. This makes is rather unlikely that a simpler model, that eliminated these would have been descriptively adequate. However it does not rule out the possibility that there are other aspects that might turn out to be unnecessary to produce the desired outputs.

MABS models allow for a finer-grained comparison than traditional ‘black-box’ models. If the outputs from two ‘black-box’ models are the same given identical inputs, then they are functionally equivalent. In contrast MABS models allow for comparison at finer-grains both in time and in detail. Thus, for example, if two models differ significantly in the behaviour of individual agents as they interact then they are different, as with different interactive processes that generate the same aggregate outcomes.

This means that it is extremely unlikely that any simplification of a MABS model will result in a completely equivalent model. Even when the results appear to be indistinguishable within a particular range of parameters and set-ups, it is likely that, with enough ingenuity, it will be possible to find some settings and initialisations that will force any two different models to diverge in terms of behaviour, and if this is then run for long enough this divergence will become statistically significant. Even if the same algorithm is implemented on two different systems, there will be details such as the nature of the floating-point representation and random number generators that would eventually cause detectable differences [1, 14].

Thus the aim of simplifying models should not be that they retain all the behaviours of the more complex model, but rather that they retain all relevant behaviours. So before one attempts simplification, one has to decide exactly what it is about the behaviour that is considered significant. Then one can investigate how one can simplify models whilst preserving this behaviour. One corollary of this is that it may well be that different simplifications will be appropriate when the same model is used for different purposes or in different contexts. This context-dependency of simplification is opposite to that in the KISS approach, for there one makes a model more complex in order to be less general.

The difficult part in science is not finding attractive abstract models, but of relating abstract models to the world (i.e. the target domain). The KISS approach ensures that one has an attractive and understandable model, but does not (of itself) give any reason to suppose that it will lead to models that relate strongly enough to the target domain so as to usefully inform us about that domain. The KIDS approach starts with a model which relates as strongly to the target domain as possible, but does not ensure that the models are "elegant". Before the advent of cheap computational power, it was only possible to get any results out of analytic (and hence relatively simple models), this made the KIDS approach infeasible.

The trade-off between the practicality of our models and their descriptive adequacy is a complex and context-dependent one – as with all modelling decisions, there is no final and general answer [9]. Neither the KISS nor the KIDS approach will always be the best one, and complex mixtures of the two will be frequently appropriate. However the balance is shifting away from KISS and towards KIDS in areas dominated by complex phenomena. In such areas there is no reason to suppose that elegant models will be particularly useful and the advent of MABS facilitates the creation, management and communication of complex, descriptive models.

In short, when modelling multi-agent and multi-actor systems, (where there are many good reasons to suspect that things will be very complex), one would need strong reasons for adopting a KISS methodology – much better reasons than empty invocations of "simplicity". In science, at least, truth comes before beauty.

We would like to thank the many people with whom we have discussed these issues, including: Tom Downing, Juliette Rouchier, Jim Doran, David Hales, Rosaria Conte and Guillaume Deffuant. We would also like to thank the anonymous referees whose queries have provided us with the perfect excuse for citing so much of our own work.