The Purpose and Place of Formal Systems in the Development of Science

Bruce Edmonds

Centre for Policy Modelling,
Manchester Metropolitan University
http://bruce.edmonds.name

Prologemma –Newton’s use of formal systems

Perhaps the most important legacy of Newton is in the use of formal systems.  He established, for the first time, a close mapping between a formal system and a set of aspects of our world. This mapping allowed complex inferences to be made about many different aspects of the world. This went beyond merely exploring mathematics for its own sake and beyond using mathematics to merely express relations found in data. In fact, the mapping seemed to be so accurate in so many different ways, explaining so many diverse phenomena, making so many novel yet correct predictions about the world and bringing together so many different types of phenomena together into a single descriptive framework, that it was taken (with some justification) for the literal truth. Here the full potential of formal systems was revealed.

As it happens, Newton did more than discover this mapping, he also invented a system of mathematics for the mapping to go to (as did Leibniz). He presented his system in a pseudo-axiomatic form - the three Newtonian laws. When his theory is taught, it is the formal part that is brought to the fore, since for people today this is the less obvious and more difficult part.  The overriding importance of the mapping between his system and the world is now less prominent. Shallow imitations of Newton’s method concentrate upon inventing new formal systems, treating the mapping into the observed world as a secondary concern.  The result of such imitation is technical brilliance along side almost complete irrelevance. 

The aim of this paper is to re-emphasise that the purpose of formal systems is to provide something to map into and to stem the tide of unjustified formal systems.  I start by arguing that expressiveness alone is not a sufficient justification for a new formal system but that it must be justified on pragmatic grounds.  I then deal with a possible objection as might be raised by a pure mathematician and after that to the objection that theory can be later used by more specific models.  I go on to compare two different methods of developing new formal systems: by a priori principles and intuitions; and by post hoc generalisation from data and examples.  I briefly describe the phenomena of “social embedding” and use it to explain the social processes that underpin “normal” and “revolutionary” science.  This suggests social grounds for the popularity of normal science.  I characterise the “foundational” and “empirical” approaches to the use of formal systems and situate these with respect to “normal” and “revolutionary” modes of science.  I suggest that successful sciences (in the sense of developing relevant mappings to formal systems) bare either more tolerant of revolutionary ideas or this tolerance is part of the reason they are successful.  I finish by enumerating a number of ‘tell-tale’ signs that a paper is presenting an unjustified formal system.

The Justification of Formal Systems

By themselves formal systems tell us nothing, since we can construct them with whatever properties we desire. It is easy to get the impression that they inform us of the consequences of our assumptions (or conversely the assumptions behind our reasoning) but this is not the case. A formal system only relates its assumptions to its conclusions via its inference rules and in general we are free to choose these rules as we like.

Some formal systems are so general (or equivalently so expressive) that we can use them to capture any other formal system (as far as we know), examples include: set theory, type theory and category theory (Marquis, 1995). In each of these, other formal systems (including each other) can be embedded. The bare fact that one is using one of these general formal systems tells us nothing about what is being formalised unless something about the nature of the relationship between the formal system's entities and the object of modelling is specified. (Sometimes this relationship is specified by a default interpretation, typically derived from the context of the formal system’s original development.)

Such general systems only derive explicit content when they are constrained in some way.  This constraint can be achieved by the specification of additional information in the form of assumptions or by mapping part of the system into a more restricted system. The more constrained the systems are, the more explicit content they have but the less general they are – there is an inescapable trade-off between generality and the amount of content (although this trade-off is not necessarily simple).

However, formal systems also have implicit content derived from their structure. The structure of a formal system makes it easier to formalize certain kinds of subsystem - those whose structure somehow 'suits' that of the general system. This means that for any being with limited resources (at any one time) the choice of formal system will affect the difficulty of formalizing something. That is, a formal model of something will almost certainly be more difficult in one formal system than in another. To put it another way, the model that results from being formulated within one formal system will be more complex than that formulated in another. Thus our choice of formal system will inevitably bias our modelling efforts (impeding them in one direction and facilitating them in another). This is the reason we need different formal systems – otherwise we would use just one general system (e.g. set theory) for everything.

There is no need to invent more expressive formal systems, nor does this seem possible.  The purpose of developing new formal systems is thus entirely pragmatic.  That is to say it is useful to develop new formal systems in order to facilitate the formalization of particular domains.  It could be that a new formalism can make a certain type of model simpler, perhaps making this feasible for the first time.  Alternatively it might make the mapping of the formalism onto the domain of modelling easier and more natural, and thus provide a readily accessible meaning for the formal expressions. Thirdly, the properties of the formalism might be useful for manipulating or thinking about descriptions of the intended domain.

Presentations of novel formal systems (or formal systems with novel features) that only establish basic properties (like consistency or validity) and are justified purely on arguments of expressiveness should be treated with caution.  This is because we already have many such systems and it is an almost trivial matter to extend an existing formal system to make it a bit more expressive.

The problem is quite acute in some fields.  For example the realm of multi-agent systems (MAS) in artificial intelligence it is common to come across papers that exhibit a formal logic (or fragment thereof) which are used to express some aspect of agency.  Typically some of the basic properties of the logic are shown (e.g. soundness, semantics, proof theory, simple upper bounds to their computational complexity) and some argument presented as to why the increase in expressiveness is needed. Such a paper does not get us anywhere unless such a formalisation can be shown to be useful, for instance: lead to interesting theorems, make some new computations possible, have helpful properties for transforming formal descriptions or just simplify formal descriptions and manipulations in some domain.

The assessment of the appropriateness and utility of a formal system is made more difficult if its intended domain is not made clear. One common source of domain vagueness is when similar domains are conflated. 

For example it is common that the demonstration of the relevance of a formal system is demonstrated with respect to an idealization of the intended domain of application – it being implied that it will be useful in the original (non-idealised) domain without actually demonstrating this.  Such conflations are often based on the assumption that the approximations necessary for the subsequent mapping onto the final domain are essentially unproblematic. An indication that a paper is focused on idealisations is when a system is demonstrated only upon “toy” problems or otherwise artificially simple cases.  Another tell-tale sign is when it is assumed that the extension to “scaling-up” to realistic examples will be unproblematic or is simply listed under “further research”.

An Argument Against

However, a mathematician (or logician or whatever) may object in the following manner: “the history of the development of formal systems has included many systems that would have failed on the above criteria and yet turned out to be immensely useful later on  - are you not in danger of preventing similar advances with such warnings?”. My answer is fourfold.

•              Earlier, we did not have the huge number of formal systems we have today, and in particular the general systems mentioned above were not mature.  Today we are overwhelmed by choice in respect to formal systems - unless substantial advances are made in their organization all new systems will need to be substantially justified if their clutter is not to overwhelm us.

•              There is a proper domain for formal systems that do not relate to a specific domain using one of the criteria specified above: pure mathematics.  Presenting a formal system elsewhere implies that it is relevant in the domain it is being presented in.

•              Even in pure mathematics presentations or publications are required to justify themselves using analogues of the above criteria - novelty, expressiveness and soundness are not enough (although the other criteria perform a weaker role than when they are applied elsewhere).  For example, in the examination of a doctoral thesis in pure mathematics once the soundness of the work is deemed acceptable it is the importance, generality and relevance of the results that are discussed.

•              The cost structure of the modelling enterprise has changed with the advent of cheap computational power.  It used to be the case that it was expensive in both time and other resources to use and apply a formal theory, so that it was important to restrict which formalisms were available.  Given that the extensive verification of the success of formal systems was impossible they had to be selected almost entirely on a priori grounds. Only in the fullness of time was it possible to judge their more general ease of use or the utility of their conclusions.  Now this situation has changed, so that the application of formal systems has been greatly facilitated using computational techniques.

Chains of Models

Another possible objection that might be raised is that a particular theoretical system is the starting point and that others will then apply this in directly useful and testable models and simulations.

It is true that one may need to employ more than one model in order to capture a particular phenomenum. In fact it is common to have whole chains of models reaching from the most abstract theory down to the most basic data. At the bottom is the object or system that is being modelled (e.g. the natural phenomena one is concerned with).  From this data may be obtained by the process of measurement – so at the next level up one may find a data model.  At the other extreme there might be some fundamental law or system that a formal model has to be consistent with – this may be as abstract as a system of definitions or the syntax of the formal modelling framework. Each model in the chain has to relate to the models “above” and “below” it via the relations of validation and verification (see figure 1).

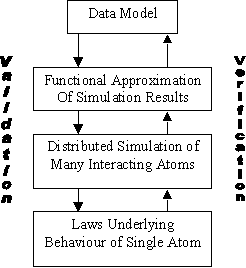
Figure 1. A chain of models from data model upwards (abstracted from an actual example in chemistry)

One model validates another when it specifies some constraints that the second model must obey - for example: a model of chemical interaction has to be consistent with atomic physics.  Thus validation provides a prior constraint upon a model - for it constrains the design of a model.

One model is verified by another when the predictions or output of the model is shown to be consistent with the second model.  For example a law may be verified against a set of data if it predicts the data with sufficient accuracy.  Thus verification is a post hoc constraint upon a model - it determines whether a complete model is in acceptable agreement with another (usually a model closer to the target phenomena).

Such chains of models are a common and natural means of dividing the design, implementation, checking and justification of complex models into manageable steps.  It does mean that in many domains it may be impractical to verify the utility and relevance of formal models immediately. Such  verification might require a combination of models, as just described.  These chains of models are discussed more in chapter 2 of (Edmonds 1999b)

In such situations, although one may not be able to exhibit a final justification of a formalism in terms of the criteria above, one can provide some justification by establishing its coherence with its theoretical context (its validation) and some verification against a model that is as near to the grounding phenomena as possible.  This could be necessarily only a step towards a finally convincing justification, which would occur when the complete chain of verifications, all the way down to the target phenomena, is completed. However, until the chain is completed it might be wise to retain a level of agnosticism as to the appropriateness of the model since it could turn out that the model does not relate, even indirectly, to the target phenomena. That such a complete verification has been repeatedly put off it can be taken as evidence that either people have failed in their attempts to complete it or even that this has seemed too difficult to attempt. A formal system which can boast of no thoroughly verified models, and thus currently unproven is much closer to an unfulfilled intention than a successfully executed plan.

A Priori vs. Post Hoc Formalization

One common method of establishing the relevance of a formal system is to justify the system's design with reference to a set of abstract principles. These are typically a priori principles, that is they are decided upon the basis of intuitions or tradition prior to the verification of the system against the problem or domain of study.  This is in contrast to a post hoc formalization where one is trying to generalize from a substantial series of observations or trials in the domain of study.

In general post hoc formalisation is greatly to be preferred to a priori formalisation. The reason for this is that as soon as one starts to use a formalisation this tends to bias one's perception of the phenomena or problem under study. To apply Kuhn's term, one’s observations are “theory-laden” (Kuhn 1962), because one can not help but view the basic data through the “lens” of the theory or formal system one is using. One cannot escape the fact that any formal system has implicit content as described above – it will inevitably make some models easier and others more difficult. If one is attempting an a priori formalisation then the chances of it happening to bias ones efforts in the best direction is very small because one is guided only by one’s intuitions.  In post hoc attempts, one already has a body of data drawn directly from the phenomena under question in order to constrain and guide the direction of ones efforts.  The problem domain itself is likely to be a better guide to that domain than intuitions gained over other problem domains, especially if the domain under study is new.

Great post hoc formal systems are sometimes associated with “revolutions” in science.  A new theory is proposed outside the framework of established theory that explains and/or predicts a wide set of observed phenomena or solves a wide set of existing problems.  If the new theory is sufficiently successful compared to others it may come to be accepted as the new established theory. Examples of this are the Newtonian theory of gravity and the plate tectonics revolution in geology.

At other times “normal science” prevails. Researchers in these periods seem to work largely within an established theoretical framework, building on each other’s work by solving complementary problems. The danger of this is that a field can become closed to outside influence and contrary findings. It thus immunizes itself to falsification to some extent and limits the invention of new theories and formalisms to those consistent with the established paradigm. Thus although such periods of science can be very efficient and productive, the simultaneous weakening of selective pressure from outside the field and the lessening of the variation inside means that it can become sterile once it has exhausted the domain of applicability of the established framework.  If this established framework is very general and successful then the span of productive work within the paradigm can be long, but if it is limited in generality and poor at explaining and predicting the target phenomena then it may only have a stifling effect upon the development of knowledge.

Social Pressures and Embedding

It is interesting to note that an analogous process can be observed among co-evolving populations of adaptive social agents.  When the complexity of their environment is great they may come to rely on the outputs of other agents as effective “proxies” for aspects of that environment. This occurs when constraints on their rationality mean that the full modelling of their environment is impractical and hence the social proxy is a useful substitute (despite its relative unreliability). If a substantial proportion of the agents in a population use each other's outputs as such proxies the development of knowledge can become somewhat self-referential within that population. Elsewhere I have investigated this effect using simulations of this phenomenum, which I called “social embedding” (Edmonds 1999a). When it occurs it can increase the computational efficiency of that population but also means that the absolute success of that population may drop slightly over time (especially if only relative success among the agents is important to the participants, as in competitive situations). 

In my simulations (Edmonds 1999a) I found that new agents (or new models introduced by existing agents) typically either do relatively badly when introduced to the population or (more rarely) very well.  The new agents are not well embedded in the society and hence can not immediately make use of the computational resources implicit in the available “proxies” (since they do not know how to use or interpret these). However they may happen upon a better model than those current in the established population due to the fact they are not embedded.  If the model is much better than existing models it will do much better than the rest and quickly become established as a proxy for use by others. If its models are only marginally better, their objective superiority may not be sufficient to counter-act the efficiency of the embedded computation occurring in the population. In this latter case the model may eventually be discarded despite its marginal superiority in conventional terms.

Figure 2 below is an illustration of some of the causal links between each agent’s best models (represented by a single box) during the last three time periods of the simulation.  A line means that a model explicitly uses the output of a previous model.  For some of the models (indicated by a high number in the box) their results depend upon the results of several previous models that themselves depend upon previous models etc.  In fact this chain stretches back over a very large amount of time and involves a large proportion of the total population.  In such cases it is sometimes much simpler to explain the actions and in terms other than the detailed web of reference and the explicit content of the models if taken alone.  The practical effect and meaning of the agent’s models comes from the web of social interaction to a considerable extent.


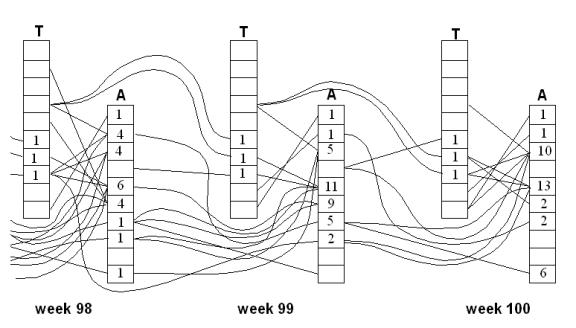
Fig. 2. A causation network going back over the simulation time at the end of a simulation (from Edmonds 1999a)

Such models illustrate why it could be a lot more comfortable to participate in a process of “normal science”. Once one has become accepted into a field (i.e. becomes embedded in it) one can participate in a complementary process of problem solving, by specialising in a certain area and building on each other’s work. The efficiency of a socially embedded group, its accompanying tendency to encourage specialisation and the provision of an established framework mean that one’s work is far less onerous. The fact that others may come to accept one as a “proxy” in certain areas means that one’s status (and hence ones job) is relatively secure. Here the picture is of a communal building-up of a wall of knowledge: each brick needs careful checking so that it can support those that will be placed on top of it.

A life pursuing “revolutionary” science is much less comfortable. One does not know how one’s ideas will fare – they may succeed if they are significantly better than existing models to justify their acceptance or they may completely fail. Rather than participating in a complementary process of specialised problem-solving one is involved in sharp competition. Unless one succeeds in causing minor revolutions one will have to endure being permanently relegated to the fringes. Here we have more of an evolutionary picture: a constant stream of new variant models and theories are being produced which are then weeded-out according to their acceptance amongst peers – instead of being built-up, knowledge is constantly being adapted to meet current needs.

Clearly these different modes of science will attract and be suitable to different types of people. Both processes are needed and hence both types of people are needed. The ideal (viewed from outside) would be that: “normal science” should predominate in areas where an empirically successful theoretical framework has been found (e.g. chemistry), so that the maximum possible benefit can be efficiently extracted; while “revolutionary science” should be encouraged in areas where empirical progress is inadequate (e.g. economics).

Unfortunately, it often seems to occur the opposite way around: empirically unsuccessful sciences (the “degenerate research programmes” of Lakatos 1983) seem to covert the garbs of “normal science” in order to claim academic respectability whereas successful sciences display the confidence to allow the presence of revolutionaries. Of course, this may be the wrong way around: it may be that allowing revolutions is necessary for the success of a science, due to the stability of highly embedded groups and the self-justifying nature of theoretical frameworks, and that fields which constrain progress to small advances within established frameworks inevitably stagnate.

Foundational vs. Empirical Approaches

The approach whereby one starts by postulating quite abstract, a priori principles and then tries to demonstrate that, with the addition of auxiliary assumptions, that the consequences are adequate to the domain of study can be called a “foundationalist” approach. An approach with more emphasis on starting with the observations or problems derived from the domain of study, postulating appropriate models for each of these and later generalizing these to theories can be called an “empirical” approach.

Both the foundational and empirical approaches are only completely successful if they complete the chain all the way from problems or observations in the domain of study up to some more generally applicable theories (as described above).  If the foundationalist approach achieves only weak verification against “toy” problems then its relevance remains in doubt.  If the empirical approach does not manage to achieve generality to the extent that aspects of a model for one situation are applicable to another situation then it is not very useful.

Both approaches have their part to play.  The foundationalist approach has had most success in well-defined and measurable domains such as mathematics, physics and computer science, but even in these fields there are distinct limitations.  The foundationalist approach has also had a productive role in creating a large variety of formal systems for the empirical scientist to choose among (and a less glorious role in providing straw men to be knocked down).

The empirical approach has been more successful in complex domains such as biology and the social sciences.  These are areas where our intuitions are weak and frequently misleading. This approach has the hard task of establishing reliable mappings from the real world of phenomena and problems to formal (or formal sable) theories - it is this that makes the formal system useful because it means that inference within the formal system produces conclusions that successfully relate back to the world.

Not all foundations are a priori in origin.  For example atomic physics provides empirically verified foundations for chemistry.  This has been a productive way forward - to choose foundations that have been empirically verified. This contrasts with foundations that have only weak grounding, what could be called “armchair grounding” because they could have been invented from a philosopher's armchair.

Of course, it is impossible to avoid a priori assumptions and systems altogether - one is bound to use some framework to aid one to look for data and formulate hypotheses. However this does not change the fact that the more a formalism directly relates to real observations and problems and the more flexible one can be about which formalism is deployed the better.

Simplicity – a solely pragmatic virtue

An ‘old chestnut’ that is often brought out to justify the introduction of otherwise unsupported a priori assumptions and structures is that it is for the sake of simplicity.  The implication is often that this has virtues other than the obvious pragmatic ones of making it easier to construct, communicate and analyse.  There has been a (disputed) tradition in the philosophy of science that the simplicity is truth-indicative (that is, it is something that is a useful guide to the truth).  This is traced back to William Of Occam who used the maxim “entities are not to be needlessly multiplied”.

The fact is that there is no evidence or good argument to show that simplicity is truth-indicative in general.  In fact, when machines have been set to comprehensively search all possible models in a given formal language to compare their accuracy and their simplicity on real data then it can be seen that this maxim does not hold.  Further there is an alternative explanation for why simpler models can be preferred without having to introduce a separate and mysterious connection between simplicity and truth: that it is common to elaborate unsuccessful models, which means that if one comes across a model which has been frequently elaborated then this is an indication it has been unsuccessful. Thus Occam’s razor eliminates itself!  This explains why a large part of the philosophy on this principle has been concerned with inventing different interpretations of “simplicity” in order to try and make the principle true – the principle is unsuccessful and is undergoing elaboration.

Constructivist vs. Realist Viewpoints

If the social embedding picture of “normal” science is correct, then this has the implication that the constructivist picture of their activity is, at least, somewhat valid.  The models that are developed are constrained by the product of other agents since the computational cost of always developing new models inevitably biases model development.  This does not mean that the models developed are necessarily incorrect or sub-optimal, but that the implied lack of input variety does suggest that this is probably the case.  In the simulations of social embeddedness I ran socially embedded populations did develop models that were slightly worse than non-socially embedded populations, but only by a small margin.  However it might be the case that in the long run this difference (which indicated a loss of variety) would be significant.  Socially embedded populations might eventually close in on the best models of their set but be unable to ever branch out to explore different (and possibly better) models.

Thus one can see the “revolutions” in science as ‘steps’ towards a more realistic set of models – steps where the improvement in the explanatory power of a model overwhelms the processes of social construction.  There is some anecdotal evidence that such revolutions have happened when gifted and hard-working individuals who are not socially embedded posit new models guided substantially by the observations and data to be explained rather than by other people’s approaches.

Conclusion

Just as it is important for engineers to know the strengths and weaknesses of the material with which they are going to build, so it is important That builders of formal systems know the strength and weaknesses of different methodologies.

An empirical methodology is more likely to arrive at the truth, because it starts with what is directly verifiable in the target domain. It starts with messy “phenomenological laws” (Cartwright 1983) and later attempts to draw generalizations. This requires a lot of effort both in terms of fieldwork and invention (as it is unlikely that an “off-the-shelf” formal system will work without modification).  If generalization is successfully achieved the effect may be revolutionary as it has not been developed within established frameworks.  When generalization is weak then the theories remain messy and difficult to apply.

A foundationalist approach takes much less effort or, to put it positively, is far more efficient in terms of collective effort.  It is most effective when the framework within which it works is itself empirically well-verified. In fact, the better an empirically-based revolutionary theory, the more it supports and encourages a successful foundationalist approach in its wake.  Foundationalist approaches are prone to being mislead by the formal spectacles they use to model, what they add is not so much truth content, as simplification and a framework for coordinated collective action.

A new formal system that is presented in an a priori fashion that is unjustified in terms of its usefulness in a domain has no place in the furthering of real knowledge, despite its social function and status within a socially embedded group. Such a presentations can usually be recognised by a number of tell-tale signs, including:

Acknowledgments

Scott Moss, with whom I have discussed these issues for so long that it is now very difficult to identify who thought of which idea first, Pat Hayes whose clear arguments spurred on these thoughts.

References

Cartwright, N. (1983). How the Laws of Physics Lie. Oxford: Oxford University Press.

Edmonds, B. (1997). Complexity and Scientific Modelling. 20th International Wittgenstein Symposium, Kirchberg am Wechsel, Austria, August 1997. To be published in Foundations of Science. http://cfpm.org/cpmrep23.html

Edmonds, B. (1999a).Capturing Social Embedding: a constructivist approach. Adaptive Behavior, 7:323-348. http://cfpm.org/cpmrep34.html

Edmonds, B. (1999b). Syntactic Measures of Complexity. PhD Thesis, the University of Manchester, Manchester, UK. http://bruce.edmonds.name/thesis/

Marquis, J. P. (1995). Category Theory And The Foundations Of Mathematics – Philosophical Excavations. Synthese, 103:421-447.

Khun, T. (1962). The Structure of Scientific Revolutions. Chicago: University of Chicago Press.

Lakatos, 1962Lakatos, I. (1983) The methodology of scientific research programmes. Cambridge ; NY: Cambridge University Press.

Moss, S., Edmonds, B. and Wallis, S. (1997). Validation and Verification of Computational Models with Multiple Cognitive Agents. CPM Report 97-25, MMU, UK.  http://cfpm.org/cpmrep25.html

Murphy, P.M. and Pazzani, M.J. (1994). Exploring the Decision Forest: An Empirical Investigation of Occam's Razor in Decision Tree Induction, Journal of Artificial Intelligence Research, 1:257-275. http://www.jair.org/abstracts/murphy94a.html