Emergence in and Engineering of Complex MAS
Centre for Policy Modelling,
Manchester Metropolitan University
{bruce@edmonds.name, norling@acm.org}
As far as the laws of Mathematics refer to reality, they
are not certain;
and as far as they are certain, they do not refer to reality (Albert
Einstein[1])
We discuss the implications of emergence and complexity for the engineering of MAS. In particular, we argue that while formalisms may play a role in specification and implementation of MAS, they do not provide predictive power in complex systems. Thus we must look to other tools for understanding these systems. Statistical methods may go some way to helping us, but they too have their limitations. Rather, we argue that we must revert to classic scientific method: observing the systems, positing theories and hypotheses, then testing and improving them. That the study of complex MAS has to be more of a natural (as opposed to formal) science. This has the consequence that there will be severe limitations on the extent to which one can “design” complex MAS. We illustrate this case with two examples of MAS, both of which display system level dynamics that cannot directly be predicted from the behaviour of individuals. We call upon those in the ESOA community to explicitly reject those tenets that are only useful with simple MAS.
1. Introduction
Consider farmers. They may know their animals, crops and land in some detail, but are under no illusion (recreational farmers from the city apart) that designing a farm to work well would contribute more than a small part to its success. Rather they understand that they have to always be monitoring their farm, acting upon it repeatedly to try and get acceptable results. This is not an exercise in careful planning but more of a continual exercise in disaster management. In such a situation, new ideas cannot be assessed on the grounds of reason and plausibility alone (including those suggested by scientific advisors) but have to be tried out in situ. Solutions are almost never permanent and universal but rather a series of tactics that work for different periods of time in particular circumstances. Techniques that are seen to provide real benefit (even if that benefit is marginal) are adopted by others in the community so that, in the longer run, a community of effective practices evolves. This paper suggests that in order to get complex MAS to work well we have to learn to be more like farmers and less like mathematicians.
The argument proceeds as follows: Section 2 makes clear what we mean by the ideas of syntactic complexity, unpredictability and emergence, arguing that emergent phenomena can not be formally reduced to system properties; Section 3 argues that this kind of complexity does occur in MAS-like systems and discusses some of the consequences in terms of these systems; Section 4 looks at some of the possible tactics researchers might take in tackling these sorts of systems; Section 5 exhibits some examples to illustrate the points made; and we conclude in Section 6 calling on the ESOA community to explicitly reject approaches that only work for simple MAS.
2. Complexity, unpredictability and emergence
In this section we discuss and define unpredictability, complexity and emergence wrt. MAS. In particular, we want to show that: just because a particular emergent feature is caused by the mechanisms and set-up of a MAS and that each micro-step is completely understandable in a deterministic way, this does not mean that the emergent feature is reducible to the mechanisms and set-up. It may be the assumption that “predictability” scales up from the micro to the macro that is behind much confusion in the software world. As Philip Anderson put it “More is Different” [1].
Complexity has many different definitions and meanings. This is because the complexity of a system is relative to the type of difficulty that concerns one as well as the frame/descriptive language in which that system is represented [7]. In this case we would characterise the syntactic complexity of a complex MAS system as the “computational distance” from the set-up of a MAS to the resultant behaviour at a later point in time, that is the minimum amount of computation necessary to determine a certain aspect of a complex MAS’s behaviour given the initial conditions, set-up, plans, programs etc[2]. If an easy-to-calculate short-cut to do this exists we say that this aspect of the MAS’s behaviour is simple. On the other hand if the shortest way to determine this is by running the MAS up to that point then it is (syntactically) complex. In the section below we will argue that many of the MAS that the ESOA community deals with are complex in this sense.
Clearly syntactic complexity can make it infeasible for an actor/agent with computational limitations to predict future behaviour, even if it has the full details of the initial set-up and any subsequent environmental inputs. In particular, if we wish to be able to predict the behaviour of a class of such set-ups without simulating each one then the presence of such complexity makes this infeasible to do directly. Thus syntactic complexity can be cause of effective unpredictability. Pseudo-random number generators are an example of this in practice – their syntactic complexity makes their output unpredictable and arbitrary in practice.
Emergence occurs when some significant behaviour occurs that (a) is not reducible to the details of the system set-up (otherwise it would not be new), but yet (b) is totally consistent with those details (otherwise it would not be from the system). Clearly both (a) and (b) being the case is impossible purely within a simple formal system. Rather what tends to happen is: since in a system of high (possibly infinite) syntactic complexity the behaviour is not predictable from the set-up then observed behaviour that appears significant to an observer is described in a different type of language to that of the detailed interactions in the system. Since this description represents observed behaviour of the system it will be consistent with its implementation, but because it is in a different language, it will not be reducible to descriptions of the implementation. For example, in Schelling’s model of racial segregation [26] the implementation is in terms of counters on a checkerboard and when they move, but the emergent behaviour that of the global segregation observed as a result, even at high levels of tolerance [13]. This is illustrated in Figure 1.

Figure 1. Emergence resulting from syntactic complexity plus abstraction
3. Complexity in MAS
Emergence and unpredictability are inevitable features of complicated systems (including MAS), even if they are deterministic and perfect implementations of the programmer's intentions. This can be seen be looking at some formal systems which, although simpler, than most MAS can be easily mapped into MAS.
In [27] Wolfram exhibits a Cellular Automaton (CA) which produces a seemingly random binary sequence in its central column, in a deterministic manner from a given initial state. Of course, since this is a deterministic system and one has “run” it before with a particular initial state then one knows (and hence in a sense can ‘predict’) what sequence will result, but if one only knows what resulted from similar (but not identical) initial states then there seems to be no way of knowing what will result before hand. Of course this is true of any pseudo-number generating program, the point is that, in this case, it would be easy to design an MAS with the same properties using essentially the same mechanism, so that what it had done in the past would be no guide as to how it behaved the next time.
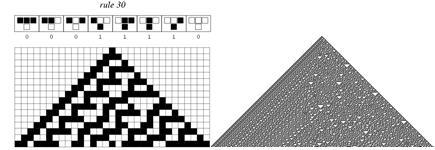
Figure 2. CA rule 30 whose central column is essentially random (left shows rule and detail)
Of course it is very difficult to prove a negative, namely that there is no “short cut” to determining such a system’s behaviour without doing the whole simulation. So, despite the available evidence, it is always possible for people to simply assert that there must be some way of doing this. However there is formal evidence against such a hope in the form of Gregory Chaitin’s proof that there are mathematical truths whose simplest proof is as complicated as the truth itself [6]. For these truths there is no short-cut, no underlying, simpler reason why they are true. In fact Chaitin’s construction shows that all but a vanishing number of such truths are like this, so that those that are explainable by a simpler construction are the tiny exception.
These sorts of results are basically versions of Gödel’s results [15]. In a sense Gödel’s results went further, they showed that (for most kinds of systems that MAS represent) that there will be true properties of such systems that are not provable at all! That is that one might (correctly) observe properties of such a system that are not reachable in terms of a formal approach. In MAS terms that means that there may well be some emergent properties of deterministic MAS as they run that can not be proved within any particular logic or formal system. Similarly Wooldridge shows in [29] that, even in finite MAS the design problem is intractable (PSPACE complete).
Of course, the situation is even worse in the real world where there are essentially non-deterministic factors from a variety of sources, including: actions from actors/agents of unknown composition and goals, random inputs, chunks of legacy code which have insufficient documentation but are still used, bugs, and machine limitations. That computer systems of any complexity have unpredictable and emergent features, even isolated and carefully designed systems, is part of our everyday experience. That it is even more difficult to get complicated MAS systems to behave in a desirable way than traditional isolated and deterministic code is also part of our everyday experience.
Indeed Nick Jennings explicitly suggested that we stop MAS becoming too complicated in order to try and maintain the effectiveness of the design tactic. For example, in [22] his advice includes (among others):
• Do not have too many agents (i.e. more than 10);
• Do not make the agents too complex;
• Do not allow too much communication between your agents.
These criteria explicitly rule-out the kind of MAS that are studied in the ESOA/ESOS community as well as all those in any of the messy environments characteristic of the real world where they may be used. These rules hark back to the closed systems of unitary design that the present era has left way behind. What is surprising is not that such systems are unpredictable and, at best, only partially amenable to design-based methods but that we should have ever thought that they were.
4. Responses to complexity in MAS
So, given this situation, what can we do to try to get complex MAS systems to behave within desirable constraints? We consider some of the possibilities below.
The formalist answer is to attempt to use formal methods to make the engineering of MAS scientific. As Wooldridge says in [28] just after pointing out the difficulty of validating the BDI framework: “Fortunately we have powerful tools to help us in our investigation” and goes on to discuss BDI logics. This is not and cannot be a sufficient answer. Rao and Georgeff noted some years earlier, there is a considerable gap between BDI theory and practice [25] and [12] proved that formal methods are insufficient for the design of any but the simplest of MAS (e.g. those without arithmetic). Hence complete formal verification is only possible for the very simplest MAS components and almost no MAS systems that would help solve real world problems. However formality can help in some more mundane ways, namely:
1. Providing a precise and lingua-franca for engineers for specifications and programs (allowing almost error-free communication);
2. Allowing for specifications and programming to be manipulated in well-defined and automatic ways;
3. Facilitating the inclusion of consistency checks within code to prevent or warn of some undesirable outcomes;
4. Provide a stable and expressive framework/language for developers (or community of developers) to gain experience and expertise in.
What is important is to abandon the delusion that formal proof will ever be a major component in generating or controlling the complex system level behaviour that we see in real world problems.
The statistical approach is another way of getting at apparently disordered systems. The first step is assuming that the system can be considered as a set of central tendencies plus essentially arbitrary deviations from these. The idea is that although one might not be able to predict or understand all the detail that emerges from such a system this does not matter if there are some broad identifiable trends that can be separated from the “noise”. Thus far is fairly uncontroversial[3], but more problematic is the next step typically taken in the statistical approach, that of making assumptions about the nature of the noise, usually such as its independence, randomness or normality. That these are suspect for complex MAS is indicated by systems which exhibit “Self-Organised Criticality” (SOC) [3]. [23] list some criteria which indicate when SOC might occur. When these are interpreted as a MAS they come out as:
· Agents are metastable – i.e. they do not change their behaviour until some critical level of stimulus has been reached;
· Interaction among agents is a dominant feature of the model dynamics;
· Agents influence but do not slavishly imitate each other;
· The system is slowly driven so that most agents are below their critical states a lot of the time.
Clearly this includes many MAS. In such systems, one can not make the usual assumptions about the nature of any residual “noise”. For example when one scales up Brian Arthur’s “El Farol Bar” model [2] to different sizes and plots the variation of the residuals it does obey the “law of large numbers” as it would if it were essentially random. That is the proportion of the variation to the system size does not reduce with increasing systems size, as would happen if the residuals were random, but a substantial residual variation remains. This is shown in [8] which was suggested by the results of [24]. In this model a fixed number of individual’s have to decide whether or not to go to the El Farol Bar – basically they want to go if others do, but not if many others want to go. They make their decision in a variety of ways based upon the past history of attendance numbers. This sort of system results in a sharp (SOC) attendance patterns around the “break-even” point. The variance in this attendance is plotted in Figure 3 – one can see that this shows no evidence that the variation around the central tendency is dropping as a proportion of system size as the system gets larger. This means that the “noise” is not random and its distribution may well have undefined moments (which can invalidate many standard statistical techniques such as regression).
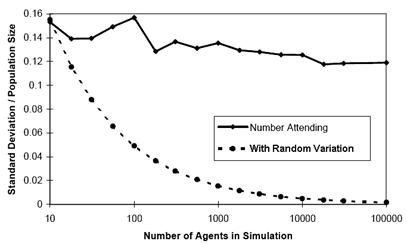
Figure 3. A plot of scaled standard deviation against different population sizes averaged over 24 runs over 500 cycles for each point in the El Farol Bar model [2]. The solid line connects the observed values; the dashed line what one would expect were the deviations were random.
Here care should be take to distinguish between descriptive and generative statistics. In descriptive statistics one is simply describing/summarising a set of known data, whilst in generative statistics a data-generating process is encapsulated which is supposed to be a model of an observed data stream. Thus, in the latter case, there must be some sense in which the statistics are a model of the source of the observed data. So, for example, if one does have a SOC system which is producing a stream of data with no defined second moment, then positing a distribution with a defined second moment would be a fundamental misrepresentation. Whereas any finite set of data obtained from this source will have defined second moment, which might be a meaningful description of the data form some purposes (e.g. in comparison with a different set of data from the same source and with the same length).
The infeasibility (and even impossibility) of using formal or statistical techniques to predict what a complex MAS will do based on fundamental principles leaves us with a problem, namely: what can we do to understand and manage complex MAS?
The short answer is the use of the classic scientific method: observing MAS, positing theories and hypotheses; then testing and improving them. In this case the “theories” usually consist of simulations at different levels of abstraction[4] and the hypotheses usually expressed in the “higher-level” descriptive framework described above. Indeed there will typically need to be a series of simulations at different levels of abstraction. This multi-layered simulation approach was suggested in [9] (among others) and put into practice in [20], where a sequence of simulations models goes from the abstract to real applications. In this way the understanding of complex MAS would become more of a "natural" (as opposed to formal) science.
5. Examples
The following examples serve to illustrate the points made above within practically realisable settings and systems.
5.1 Population Dynamics in Tag-Based Group Maintenance
This example is a evolutionary simulation of cooperation among essentially selfish but specialised individuals, with the added structure of observable (but initially arbitrary) “tags” [21]. This is continuation of a stream of research (e.g. [16], [17], [18], [19]) mostly done by David Hales. This simulation is a plausible abstraction of any evolutionary MAS with limited resources and where there are specialised skills – so that the dynamics seen in this simulation could well occur in observed complex MAS. The point of exhibiting this in this paper is not the detail of the substantive results, but that the characteristics where not predictable before doing simulation experiments but amenable to hypothesis after observation of the simulation results.
The simulation has the following characteristics:
· There is a varying population of individuals, each of which has a particular skill {1,… numSkills}, an observable “tag” in [0, 1], a tolerance value in [0, maxTol], a store for each kind of resource [0, maxStore];
· Individuals can harvest, store and redistribute a limited stream of resources into the model of several types;
· Individuals can only harvest the type that corresponds with their skill, but can receive, store and redistribute any type;
· Whether individuals survive and/or reproduce depends upon their level of resources (survive if all types > 0, reproduce if all > 4);
· Each cycle the following occurs: each individual gets an equal share of the available resource type depending on its skill; is randomly paired with a fixed number of others and donates any excess of any resource (>5) if their tag is strictly within their tolerance value of its own; individuals die; individuals reproduce with possible mutation of tags and tolerances.
Thus to survive and reproduce one has to receive donations from others with resources who have sufficiently similar resources. There is a social dilemma here: it is in the interest of individuals to have a small (or even zero) tolerance and not donate resources to others, but to have a tag ‘close’ to others with a sufficient tolerance so as to receive donations. The point is of the simulation is whether and how groups with similar tags arise (“tag groups”), in other words if and how mutual cooperation occurs. To summarise the results: groups of cooperating tag groups do arise and survive for a period but eventually collapse until another group arises. A more detailed account of this model is given in [11].
To give a flavour of some possible resultant behaviour we show the results from a single run (with the following parameter values MaxReservoirSize=7.5; MaxTollerance=0.1; FoodEachCycle=200; NumSkillTypes=3; NumPairingsPerCycle=6; ProbMutuation=0.05).
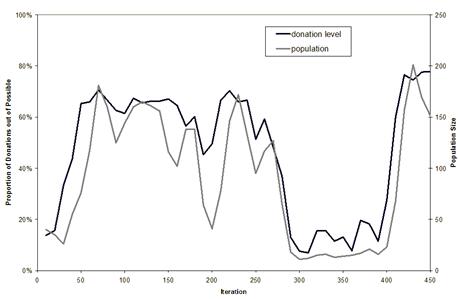
Figure 4. The population size and donation level (proportion of pairings that result in a donation) during the first 450 cycles of a run of the simulation.
Figure 4 shows the population size and donation level during the first 450 cycles of the simulation. One can see that after 50 cycles the donation level (and hence the population) rises to relatively high levels. The tight coupling between donation level and population level is due to the fact that death and reproduction is hardwired to individuals having the kinds of nutrition they can only obtain via donation.
On examination of statistics like those shown in Figure 5 and visualisations of the individuals in the population as it develops, one can distinguish some different “phases” of the dynamics: (UV – unviable) where there is not significant donation so that the population is not in a self-sustaining state; (CE – coexistence) where the cooperative group of different subpopulations has been established; (PP – predator-prey) where parasites (those with sufficiently small tolerance that they do not donate to anyone) have arisen and thus predator-prey dynamics increasingly dominate the dynamics until the population become unviable again. That these phases occur and their nature are fallible hypotheses and are not provable from the set-up and initial conditions. However now that they have been observed in many runs and set-ups then they can be modelled (to greater or lesser accuracy) based upon the understanding gained from that observation (and hopefully independently tested).
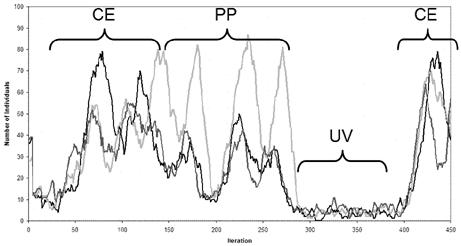
Figure 5. The number of individuals with each of the three skills in a sample run (the three lines of different shades of grey), illustrating some of the phases that can occur. CE – coexistence; PP – predator-prey; and UV – unviable.
Obviously if one was designing a similar MAS from scratch and wished to exploit the properties above, then the described simulation would be little more than a guide or analogy. If one wanted a more reliable translation into the MAS then a more realistic simulation – somewhere between the abstract simulation above and the target application – would need to be built. Thus we would have a hierarchy of models and implementations going from abstract hypotheses (possibly expressed in terms of population dynamics models of ecology) down to actual implementations. This hierarchy is illustrated in Figure 6.

Figure 6. A possible hierarchy of models and implementations
The downside of this approach, is that it does not provide any certainties, any proof, that any particular theory will be useful for creating/managing a particular complex MAS, but rather one ends up with a set of fallible hypotheses, models or “rules of thumb” which can be used to guide system creation or management but which have to be tried out to check that this is, in fact the case. An example of this is [14] which suggests the fallible rule of dealing with cases where there is conflict between agents.
5.2 Population Dynamics in Simulated Food Web Evolution
This example involves a simulated ecosystem of abstract "species", where each species is defined by a set of features that, when compared against the features of other species, determines 'who eats whom.' The individuals feed based on these rules, reproduce when they have sufficient resources, and die either when another individual kills them, or they reach old age. The example is an agent-based simulation that is inspired by a system dynamics model of the same scenario [5].
The features that are used to determine species can be conceptualised as things such as ‘sharp teeth’ or ‘fast runner;’ features which potentially could give the species an edge over other species. As in Caldarelli et al.'s model, these features are defined abstractly, with K possible features, from which each species draws L features. Following the original, we have used K=500 and L=10. To determine how each of these features fares against others, a KxK matrix is constructed and each position in the matrix is assigned a score with mean 0 and variance 1, where the value at (i,j) gives a score of how well feature i performs against feature j. The matrix is anti-symmetric (value (i,j) is the negative of (j,i)), and the diagonal has value 0. The score of one species against another is determined by taking the sum of the scores of the individual features, that is:
![]()
A single step in the model consists of:
1. If the population is 0, a new individual is created, with a random new species.
2. With some low probability, a single agent in the population is mutated. This involves selecting an individual and randomly modifying a single one of its L features. This is known as a speciation event.
3. The agents in the population are shuffled, then for each agent:
a) The agent selects a prey, or the world, upon which it will feed, as follows: A random sample of n individuals is taken from the population. Then for each of the species in the sample, a weighted score is constructed dependant on the agent’s score against that species and the number of species in the sample. A weighted score is also calculated for the world resources, taking the number of available world resources and the agent’s score against the world into account. The agent then selects either an individual of the highest weighted species in the sample as its prey, or the world resources, if that has a higher weighted score than any species.
b) The prey (or the world) is consumed, with the agent receiving a proportion of the prey’s resources, weighted both by the agent’s score against that prey (or the world), representing the effort required to kill/harvest.
c) If the agent received enough resources while feeding (i.e. its total resources > 1), it will reproduce. Offspring are given 1 resource each; the agent has these resources subtracted from its own stores.
4. Agents have their age incremented and any agents which are dead (due to being killed by a predator or through old age) are removed from the population.
This is a very simple model of food web evolution which is in its early stages of development, and although it is not clear yet how well it mimics naturally occurring food webs, it does display some behaviour which is expected yet unpredictable.
As can be seen in Figure 7, many of the species that are created in speciation events fail to find a niche within the food web in which they can survive. Others appear to find a niche, but experience sudden catastrophic declines in population. (Caused usually by over-harvesting their prey, or sometimes when a new species harvests the same prey more efficiently.) Still other species experience ebbs and flows in their population yet manage to survive for extended periods.
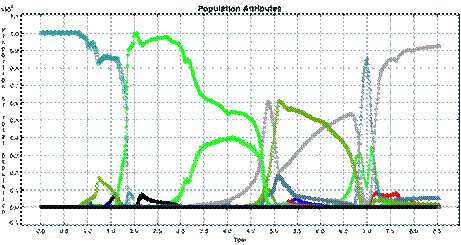
Figure 7. The rise and fall of populations plotted as a proportion of the total population against time (in 100 of cycles)
These types of patterns in the dynamics are not unfamiliar in fossil evidence, so in this sense they are expected. However whether or not a speciation event will lead to a successful species depends very much on what other species are present in the population, and at what levels, at the time of its inception. While it might be possible to determine the reaction of the food web to the introduction of a particular species given a particular state of the web, the overall dynamics of the system cannot be predicted. Indeed, this reflects problems that are seen in the natural world, when foreign species are introduced into an ecosystem (either "accidentally", as in rabbits in Australia, or deliberately, as in cane toads, also in Australia). The introduction of cane toads, as a pest control mechanism, is of particular interest. The intended result was to eliminate the pest. The ongoing situation is considerable changes to the food web of northern Australia as the toads find alternative prey.
MAS which use evolutionary techniques to achieve self-organisation will be prone to similar unpredictable population waves. Whilst these can have major ramifications for the system efficiency (especially during transition periods) they are essentially unpredictable. Learning how to manage such phenomena in complex MAS will necessitate a practical, experimental approach – the set-up of the system only provides limited information about its subsequent behaviour.
6. Conclusion
The wish for a “short-cut” to the production and control of complex MAS is strong, almost as strong as the wish for the production and control of MAS to graduate to being “proper engineering” with firm foundations in logic and formal methods. But wishing does not make things true and one can only keep up the spin that we are “almost there” for a short period of time without substantive supporting evidence.
However there is an alternative, an alternative that offers no certainties but has shown itself to be highly effective over the years – that of the classic experimental method driving the evolution, within a community of researchers, of well-defined but fallible hypotheses. There is a place for design in the production and management of complex MAS, but it is not such a prominent one – rather the bulk of the progress will rely on trying out techniques and seeing which ones work, where they work and why.
In particular we call upon those in the ESOA/ESOS community to explicitly and loudly reject those principles and approaches that are not applicable to the systems they are working with (even though they may applicable for other, simpler MAS). Namely to reject:
· That formal proof will play a major role in their production;
· That there is likely to be any “magic bullet” techniques with universal applicability for designing complex MAS;
· That the validation, management and adaptation of complex MAS are secondary matters that can be significantly ameliorated by good design;
· That the specify and design methodology is the only real way to proceed.
Reading between the lines in many ESOA/ESOS papers that I have read, I think many in this community do reject these but have not openly declared this due to their wish to avoid dissonance with others. However we argue that the ESOA/ESOS community will need to take a different path to that developed by the agent community over the last decade, putting it in the vanguard of the “software revolution” detected by Zambonelli and Parunak [30].
References
[1] Anderson, P.W. (1972) More is Different, Science, 177:393-396.
[3] Bak, P. (1996) How nature works: the science of self-organized criticality, Copernicus.
[7] Edmonds, B. (1999) Syntactic Measures of Complexity. PhD Thesis, Department of Philosophy, Manchester University, UK. http://bruce.edmonds.name/thesis/
[8] Edmonds, B. (1999) Modelling Bounded Rationality In Agent-Based Simulations using the Evolution of Mental Models. In Brenner, T. (ed.), Computational Techniques for Modelling Learning in Economics, Kluwer, 305-332.
[10] Edmonds, B. (2005) The Nature of Noise. CPM Report 05-156, MMU, Manchester, UK. http://cfpm.org/cpmrep156.html.
[11] Edmonds, B. (2006) The Emergence of Symbiotic Groups Resulting From Skill-Differentiation and Tags, Journal of Artificial Societies and Social Simulation, 9(1) http://www.jasss.soc.ac.uk/9/1/10.html
[12] Edmonds, B. and Bryson, J.J. (2004) The Insufficiency of Formal Design Methods – The necessity of an experimental approach for the understanding and control of complex MAS, in Proc. of the 3rd Int. Joint Conf. on Autonomous Agents and Multiagent Systems (AAMAS 2004). New York, New York: IEEE Computer Society, 938-945.
[13] Edmonds, B. and Hales, D. (2005) Computational Simulation as Theoretical Experiment, Journal of Mathematical Sociology 29(3):209-232.
[14] Georgé, J-P., Edmonds, B. and Glize, P. (2004) Making Self-Organizing Adaptive Multi-Agent Systems Work – Towards The Engineering Of Emergent Multi-Agent Systems. In Bergenti, F. & al. (eds.) Methodologies And Software Engineering For Agent Systems, New York: Springer (was Kluwer Academic), 321-340.
[15] Gödel, K. (1931) Uber formal unentscheidbare Sätze der Principia Mathematica und verwandter System I. Monatschefte Math. Phys. 38: 173-198.
[17] Hales, D. (2001) Tag Based Co-operation in Artificial Societies. PhD Thesis, Department of Computer Science, University of Essex.
[18] Hales, D. and Edmonds, B. (2003) Evolving social rationality for MAS using "tags", in Proc. of the 2nd Int. Joint Conf. on Autonomous Agents and Multiagent Systems (AAMAS 2003). Melbourne, Australia: ACM Press, 497-503.
[19] Hales, D. and Edmonds, B. (2004) Can tags build working systems? From MABS to ESOA, in Engineering Self-Organising Systems (ESOA 2003), LNAI, 2977:186-194.
[21] Holland, J. (1993) The Effect of Labels (Tags) on Social Interactions. SFI Working Paper 93-10-064. Santa Fe Institute, Santa Fe, New Mexico, USA.
[22] Jennings, N.R., (2000) On agent-based software engineering, Artificial Intelligence, 117(2):277-296.
[23] Jenson, H.J. (1998) Self-organized criticality : emergent complex behavior in physical and biological systems, Cambridge University Press, Cambridge lecture notes in physics: 10.
[26] Schelling, T.C. (1978) Micromotives and macrobehavior, New York: Norton.
[28] Wooldridge, M. (2000) Reasoning about rational agents. MIT Press.