Abstract
The nature and function of representation in social
simulation is analysed into the: representational; necessary; and significant.
Conditions for a reliable use of a simulation are then formulated. The special
case of numerical representation is then considered. Three simulations that
use numerical representation at their heart are discussed, one in detail. It
is found that small changes in the representation (ones indistguishable using
observation) can cause significant changes in the outcomes, and so are unsafe in
terms of informing us about the target phenomena.
Introduction – Representation
in social simulation
The question of how one represents aspects of social
phenomena is a fundamental issue for the field of social simulation. The best
way to represent any particular aspect of social phenomena depends on a great
many things, including: the goals of the modeller; the data that is available;
the techniques and facilities accessible to the modeller; and what is already
known (or thought to be known) about the phenomena. Not much is known
concerning the cognition of higher animals (including humans). To be precise,
there are no general theories of cognition that are useful at the macroscopic
level – nothing that would help the modelling of cognition. Thus a modeller who seeks to
simulate such actors interacting often has a wide choice in how to represent
the relevant aspects of their cognition in their simulations.
Now a basic assumption behind much social simulation work
is that it is useful (in some ill-defined sense) to construct simulations, even
in the case where it is not known how to represent key elements of the
phenomena (e.g. the cognition). In other words, that we can learn something
useful from simulations which include arbitrary or guessed elements.
To put it in the bluntest and simplest way, the astounding
assumption behind much social simulation is that
our simulations tell us something true even though key
elements of our simulations are wrong
Sometimes the principle of “simplicity” is invoked to
justify the modelling choices in these cases, a justification that I and Scott
Moss criticise (Edmonds and Moss 2004) as either: misleading or mistaken.
At other times it may be believed (or, more often, merely
assumed) that the exact way cognition is modelled is not critical to the
significant aspects of simulation results (what has sometimes been called the
“statistical signature”). Clearly this does not always hold (e.g. as shown in Edmonds
and Moss 2001), and critically depends upon the interpretation given to the
simulation (what is important and what is not). On the other hand, our
general experience indicates that one can sometimes model/understand
phenomena without knowing the full detail of the working of all the relevant
parts – for example, we did understand enough about breeding animals to be
useful before we knew about genetics. However, these cases tend to involve
knowledge of a vague, practical and context-specific nature developed over long
time scales, this assumption has been spectacularly less successful with
precise, theoretical and general theories developed within single lifetimes
(e.g. Neo-Classical Economic models).
Let us consider cases where we think that the exact
representation of cognition will not effect the important aspects of the
results – where we “plug in” a somewhat arbitrary cognitive mechanism (in the
widest sense) to get the simulation to work. Thus we have a simulation whose
parts are differently endorsed by the modeller: some aspects will be judged as
representative of the phenomena and some not; some aspects will be
judged as necessary to cause (within the simulation, and hence
presumably in the corresponding parts of the phenomena) the significant aspects
of the resulting simulation outcomes.
It is important to understanding the importance and
meaning of a social simulation to be clear about the following:
·
which aspects of a simulation set-up are
representative (and how);
·
which aspects of a simulation set-up are necessary
to get the significant results;
·
which aspects of the outcomes are representative
(and how);
·
which aspects of the outcomes are those that are
caused by the necessary elements of the set-up.
The way aspects of a simulation (either set-up or
outcomes) represent social phenomena may either be direct or indirect (via a
conceptual model) (Edmonds 2001).
Unfortunately, it must be said that in many papers
describing simulations these distinctions are not make clear. There is the suspicion
that, in some cases, if these were made clear the simulation would be judged as
having much less significance than is presently the case.
Clearly, if a simulation is to reliably inform us social phenomena
the following should hold:
1.
the aspects of the set-up that are judged as necessary are included
within those judged as representative;
2.
the aspects of the set-up judged necessary are, in fact, necessary to
cause the aspects of the outcomes judged significant;
3.
the aspects of the outcomes judged to be significant include those that
are judged to be representative.
In particular, non-representative (e.g. arbitrary) aspects
of the set-up should not be critical for obtaining the aspects of the outcomes
that are deemed representative. In other words, it is critical to any
conclusions drawn that any results would not significantly change as a result
of changes in the representation of underdetermined elements. The chain is
illustrated in Figure 1.
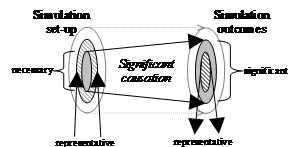
Figure 1. An illustration of
sound inference using a simulation
Of course, the soundness (or otherwise) of the steps used
to conclude something about the target social phenomena depends upon what is
being represented in set-up and outcomes (and how) as well as what is claimed
to be the significant causation in the working of the simulation. Also the
chain itself can be used in different ways, for example by attempting to
reverse engineer information about what the simulation set-up must be like in
order to get certain results.
The particular case of numerical representation
So given the analysis above the key issue I wish to
address in this paper can be formulated:
why are the difficulties of the simulation task (taken as a
whole) exacerbated by the use of numerical representation?
My answer is twofold:
1.
numerical mechanisms are often used to represent
underdetermined aspects of cognition, i.e. they are not known to be
representative;
2.
and they are brittle, in that they often cause unintended/misunderstood
aspects of the significant outcomes (“artefacts”).
Thus mechanisms such as plausible (but largely arbitrary)
functions are used to implement decision making. The classic case of this is
the optimisation over a given utility function as in many “economic-style”
models (e.g. Thoyer 2000, as criticised by me in Edmonds 2000; as well as the
examples below). I have speculated elsewhere about why this is done (Edmonds
2004), but it could be roughly characterised as either tradition or laziness.
The brittleness of many simulations with numerical
representation has now been demonstrated in many cases included within the Model-to-model
workshops. This contrasts somewhat to the case where inference is done
symbolically to obtain closed solutions in an analytic way. There the
assumptions are explicitly outlined and one has some confidence that the
results are sufficiently reliable. However in this case one has the difficulty
of relevance: social phenomena are almost always too complex for analytical
techniques to be feasible without introducing assumptions that are so drastic
that the relationship with the target phenomena is lost.
Clearly there are several possible defences to the
criticism above, including:
·
that there is some evidence that the mechanism is representative;
·
that the mechanism is not critical for producing the significant
outcomes;
·
or that there is no other feasible way of implementing the
mechanism.
Elsewhere I have argued that the use of numbers is a
difficult and dangerous choice (Edmonds 2004) and that this is not always a
necessary choice (Edmonds 2003). Here I reinforce these general arguments by
reference to some particular simulations.
The Case Studies
In this paper I report on investigations into the role of
representation in some well known social simulations: the “smooth bounded
confidence” social influence model of (Deffuant, Amblard and Weisbuch 2002);
the model of tag-based cooperation of (Riolo et al. 2001); and Hemelrijc’s
model of ape dominance interactions (e.g. Hemelrijk 2000). The first of these
will be investigated in depth, whilst the other two are only briefly discussed.
All of these simulations use floating point numbers to represent key elements
of the phenomena they are concerned with. This involves reimplementing versions
of these simulations and comparing the significant results that are obtained
when using different set-ups – set-ups that can not be ruled out by evidence
from the target phenomena (i.e. they are not representative in the above
sense).
Case Study 1: Opinion dynamics - the smooth bounded
confidence model
In the smooth bounded confidence model the opinion of an
individual on an issue is modelled as a real in a bounded interval [-1,1]. This
is supplemented by another real from [0, 1] for the uncertainty of the
individual. Further elaborations to this in a similar vein have proposed (e.g.
empathy). (Deffault et al. 2004) argue that this is an improvement upon the
simple binary Ising model due to that model’s lack of realism. However, it is
not clear that the opinions of individuals are sensibly representable as real
numbers. Rather this method of representation is, in effect, a very strong
assumption. Even stronger is the way in which opinions influence each other
via particular specified functions.
It is not argued that opinions may not be numerically
measured (or, at least, something associated with opinions) via such procedures
as surveys or voting. However this a posteriori measurement should not
be confused with a casual mechanism in a simulation. In elections the
proportion of people voting for left and right-wing parties can be measured,
but the opinions of the voters are not simply points on a single dimension but
much more complex and effected by a myriad of issues. This is evident due to
the fact than substantial proportions of lower income groups vote for
conservative parties that reduce the tax of richer groups and provide the lower
income groups with fewer benefits.
The criticality of this method of representing opinions is
evaluated by comparing the results of (Deffault et al 2002) and similar models
with very slight modifications. We will call the Smooth Bounded Confidence
model of (Deffault et al 2002), the SBC model.
In the SBC a normal function,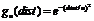 
, is used as the definition
of “influence” (between two individuals who interact whose opinions are at a
distance, dist, from each other and where the affected individual has
uncertainty, u). This is a fairly arbitrary function, if one replaces it
with a similar function 
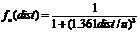one gets very different results. The
two functions are illustrated below in Figure 2. The factor of 1.361 in fu was chosen so that the functions had the same area and hence, roughly, the same overall “pulling power” (but with a slightly different shape). I will call the variant
of the SBC model that replaces the gu function by the fu,
the “inv cube” model.
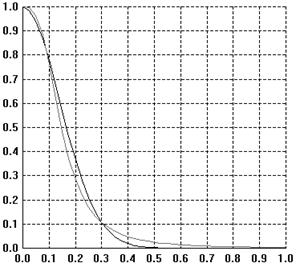
Figure 2. The gu (black) and fu (grey) functions compared
for dist in [0,1] (where u=2).
fu is slightly more
leptokurtic than gu.
Importantly this means that at greater distances fu retains some (small) significant value.
These functions are pretty close to each other, certainly
close enough that we will probably not be able to tell which is a better model
of the extent of influence between two individuals from direct observations of
those individuals. However the difference in the outcomes from the
interactions in the model is significant – one gets qualitatively different
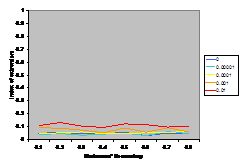
results. Figure 3 shows the output from (Deffuant et al.
2002) model using the gu function to moderate the influence
of individuals. This model starts off with two groups of 5 extremists with
opinions –1 and 1 and low uncertainty (u=0.05) and 100 moderates of a
higher uncertainty (in this case u=0.6) with a random distribution of
initial opinions. All individuals interact once with a random other each time
period. The result is that the extremists “pull” the other opinions towards an
extreme (see Figure 3 – the results are then constant from
then on).
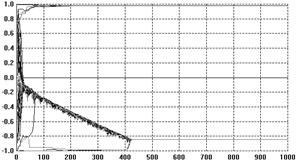
Figure 3. A typical outcome of
opinion dynamics model using the gu
function (i.e. the original SBC model), where the moderates have an uncertainty
of 0.6.
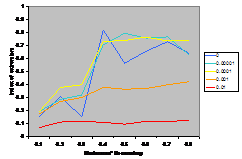
Compare this with the results from the same model, where
the only change is due to using gu rather than fu.
A typical run is shown in Figure 4. The result is that
this time, in the end, the moderates “pull” the extremists into the centre.
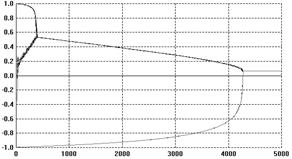
Figure 4. The corresponding
typical outcomes from the opinion dynamics model using the fu function (otherwise the
same as that illustrated by Figure 3.
Similarly if one takes the model using gu
and adds a very small amount of noise to the process, one gets different
results again. Changing this model so that there each time period there is a
0.1% chance of each individual’s opinion having some random Gaussian noise (SD
0.3) added. Thus we are changing the model so that (on average) out of about
100 people someone only changes their mind due to an otherwise unmodelled
reason only once every 10 periods. This is a very conservative amount of noise
– it is likely that, in reality, the corresponding rate is much higher! The
outcomes now change again, a typical run is shown in Figure 5.
Here one has the initial polarizing affect seen in the original model, but then
some interesting dynamics later. Over time enough individuals with “mutated”
opinions collect to form intermediate groups – that is new moderate groups are
continually spawned.
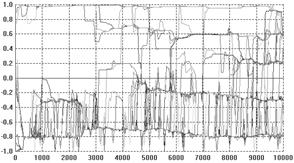
Figure 5. A typical set of
outcomes (using the SBC gu
function) where a low level of noise is added (a 0.1% probability of mutation
for each individual each cycle having Gaussian noise of SD 0.3 added)
To show that these differences are real and I have not
merely been lucky in the above examples, I ran the SBC model 25 times for every
combination of: one of five functions (SBC, inv cube, linear, 1-SBC and
constant) in both bounded and unbounded versions; moderate uncertainties of
0.1, 0.2, …, 0.7, 0.8; and probabilities of mutation of 0, 0.001%, 0.01%, 0.1%,
and 1%. That is a total of 10,000 runs of the model with 110 individuals to
10000 cycles. The functions are illustrated in Figure 6 – the bounded versions of these functions are the same but are truncated to zero for all distances greater than 3 times the uncertainty.
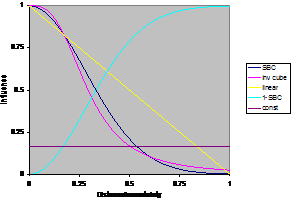
Figure 6. The different
influence functions tested for scaled distances in [0,1]. Bounded versions of
the functions are the same but truncated to zero for distances above 3 times
the uncertainty.
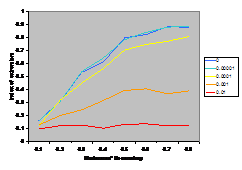
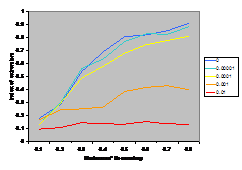
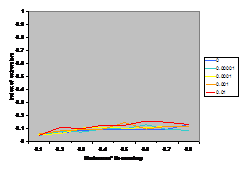
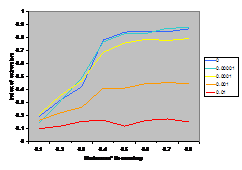
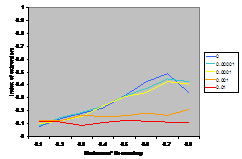
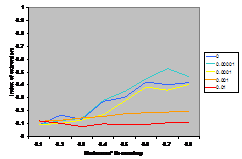
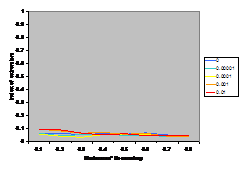
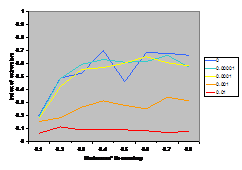
A summary of the results are shown in Figure
7. This shows the average index of extremism over the last 1000 of the 10000 cycles. This index is the size of the greatest group times its distance from the centre (i.e. its absolute value). Thus if the run ends with
many different groups or they are all in the centre the value is small. Several
paragraphs of „Current text“ follow.
There are several interesting points to note in the
results illustrated in Figure 7. Firstly, increasing noise (in the form of the probabilistic mutation of opinions as described above) decreases the extremism that results. A probability of 0.1% makes a substantial difference (see Figure 5) allowing the formation of intermediate groups and a probability of 1% almost completely eliminates any coherent tendency (including that to an extreme). Secondly, bounding the SBC and linear functions (1st
and 3rd rows, left and right) makes no essential difference to the
results – this is unsurprising since these functions essential fall to zero
before they can be bounded anyway. Thirdly, for all the other functions
(inv cube, 1-SBC and const) it makes a substantial difference to the results
(for levels of noise at 0.1% and below). Fourthly, (as noted by Deffuant,
Amblard, Weisbuch and colleagues in their papers on this) that an increase in
the moderate’s initial uncertainty increases the extremism that results, but
only for effectively bounded functions and low (<0.1% probability) levels of
noise.
Thus we can see that the SBC model of opinion dynamics is
vulnerable to slight changes in the model, e.g. that between using the SBC and
inv cube function. This change is so small that one could probably not be distinguished
between them by any direct empirical observations of how individuals actually
influence each other when they interact. This means that any cross-validation
(in the sense of (Moss and Edmonds 2005) is not possible. Thus, if we are to
preserve the structure of the SBC model, we are left with only the outcomes
that can be meaningfully validated against what is observed. Because of its
brittleness we can not use this model to explain the outcomes in terms
of what is known (or suspected) about the workings of individuals’ opinions.
In other words we are left with trying to infer something
about the working of individual’s opinions when they interact in pairs from
our validation of the outcomes. However, if different versions of the
model (e.g. using a fundamentally different underlying representation of
opinions) can produce the same outcomes (at least with the same
distinguishable outcomes in terms of what is qualitatively known/observable of
groups of individuals) then we can not even do this. However (Stauffer et al.
2004) essentially do this by producing a discretised version of the SBC model
and getting the roughly the same (and qualitatively indistinguishable)
results. Thus we are left with the conclusion that we can not infer anything
using the SBC model – it is fundamentally unsafe for inference in any
direction.
I would argue that the reason it is unsafe, is that
the opinion mechanism has no direct reference to anything directly observable
in terms of what individual’s do or the nature of their opinions. Thus there
is no way of knowing whether, for example, we should add noise or not (and if
so how much of what kind). Similar experiments with multidimensional binary or
continuous representations of opinion suggest that similar divergences occur in
the presence of small amounts of noise and/or when there is very weak
interaction between the dimensions, however that research is still at an early
stage.
One of the problems here is that it is not clear what in
the model the authors intend as essential to the model and what they
think is incidental (done simply to get the model working but thought
irrelevant to the results). More information about the intermediate conceptual
model, which these models are really about (Edmonds 2001) would help clear
up these issues. The results shown in Figure 7 would suggest that the results are fairly independent of the exact shape of the influence function except for its sharp boundedness (its “meta-stability”). Thus I would suggest that this unnecessary and
unrepresentative (in the above senses) numeric functions should be eliminated
in terms of a simple model based on the simple principle that one is influenced
only by those with similar opinions as oneself.
Case Study 2: Tag-based models
(Riolo et al. 2001) presents a model of social interaction
where individuals each have a “tag” – a socially observable cue, in a
“prisoner’s dilemma” type cooperation game, following a suggestions in (Holland
1983). In this, the tag of each individual is represented as a floating point
number, t, in [0, 1]. Each individual also has a “tolerance threshold, T,
represented in the same way. The idea is that individuals as potential donors,
D, are randomly paired with others who are potential recipients, R.
If the difference in their tags is strictly less than the first individual’s
tolerance (|tD - tR| £ TD) it donates some
resources to the other, with no direct recompense. The tolerance value
represents how selfish the individual is – a low value means they donate to few
and a high value means they donate to a wide range of others.
Surprisingly this model results in a high rate of donation
and a small but significant average tolerance value. The statistics for a
typical run are shown in Figure 8.
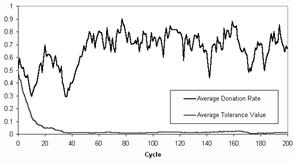
Figure 8. The donation rate and
the tolerance value in a typical run of the Riolo et al. model
However it turns out that if one changes the condition of
donation from |tD - tR| £ TD to |tD - tR| < TD
then occurrences of donation all but disappears. Figure 9
shows the output from a typical run in this case. After an initial peak of
donation it quickly dwindles to insignificant levels and the tolerance values
converge on a zero tolerance. It turns out that, in this model, the threshold
tolerance values are not important, for the “engine” of cooperation if a large
set of individuals with exactly the same tag values (“tag clones”). Members of
his set are forced to donate to each other in the original model but not
in the modified model. This fact was “masked” by the representation of tags as
floating point numbers with different degrees of tolerance. It is much
less misleading to use a (large) set of discrete labels as tags and a single
bit for tolerance. Doing this involves loosing nothing of the results and
gains much in terms of clarity. A much fuller investigation of this model is
reported in (Edmonds and Hales 2004).
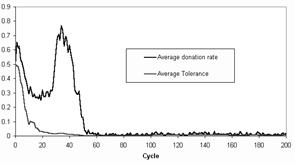
Figure 9. The donation rate and
the tolerance value in a typical run of the Riolo et al. model, but with strict
tag comparisons.
Note that, as in the opinion-dynamics case, it is not
impossible to use floating point numbers to represent aspects of social
processes, but that (1) the complexity of numerical representation can act to
“mask” assumptions upon which models work; (2) numerical representation can
have unintended affects, creating model “artefacts”; and (3) often the full
range of properties of such numbers are not needed to represent what they do
–more representative models are often possible.
In (Edmonds 2005) I exhibited a tag model which has the
same representation of tags and tolerances as that above (but where the totally
selfish case is allowed as in the second case above). However this resulted
from the exploration of more complex (multi-dimensional and/or discrete)
representations of tags that might have a more obvious genetic interpretation –
what I discovered (and this tallies with the experience of David Hales in many
papers – see www.davidhales.com) is that, in the case of tags, the
representation of tags, the distance function etc. do not make a substantive
difference to the results. As a result of this I felt justified in using a
numeric representation since it was not necessary to the results. This is one
benefit from following a KIDS rather than a KISS approach (Edmonds
and Moss 2005).
Thus with tag-based methods of group formation, it seems
that one can use a reasonably wide range of mechanisms for tags and that what
is significant about this mechanism are things like: that it is possible for
individuals not to have to be cooperative; that new groups form relatively
easily compared to the rate at which old ones are invaded; and that once
invaded old groups die. The earlier use of numerical functions in such as
(Riolo et al. 2001) served to mask these underlying distinctions leading to
misunderstandings, e.g. the “Tides of Tolerance” interpretation of (Sigmund and
Nowak 2001). This contrasts strongly to some of the simulations of David Hales
(e.g. Hales 2001) where tags are simply represented by one of a set of unique
labels.
Case Study 3: Hemelrijc’s model of ape dominance
interactions
Finally Hemelrijk’s model of ape dominance interactions is
examined. A key aspect of this model is that each individual (standing for a
single ape) has a floating point number associated with it to indicate its dominance.
During the questions after her presentation of her work (Hemelrijk 2003) at
ESSA 2003 she said that whilst some intransitivities are occasionally observed
(i.e. simultaneously A >B, B>C, and C>A) it did appear that (on
the whole) the apes did act as if each individual had a dominance level
which was discernable by others. The exact empirical grounding behind this
claim is not entirely clear. However (even though the intransitivity and the
claim are not entirely compatible) this claim has been given justification on
empirical grounds (i.e. it is descriptively accurate) and thus brings the
numerical mechanism within the representational.
In this model apes move around on a 2D surface. If they
get sufficiently close one (or both) may consider instigating a “dominance
interaction” with the other. Before doing this they mentally try this out to
see if they might win it, if they do they engage in such an interaction,
otherwise they signal submission to try to avoid this.
I reimplementated the model as reported in (Hemelrijk
2000, 2003). However this replication has been done using a very different
language and framework than that of the original and I have not been able to
get some of the results that Hemelrijk reports. Despite several requests to
her (and others) I have not been able to obtain the code to read and check the
necessary details.
Using this imperfect implementation I tested a couple of
variants in the way the update function is performed. This is the “suspicious”
part of the simulation, since the dominance number is primarily used to
implement a total dominance relation between the individuals in the model, and yet
arithmetic operations are applied to them to update this after a dominance
interaction. However, despite producing minor variation in the overall levels
of dominance, the substantive results in other respects were not significantly
altered. This indicates that either: (a) the representation is fairly robust
w.r.t. to its intended interpretation or (b) that I have not tried enough
variants. In any case the model survived this attempt to probe its weaknesses,
for I did not come up with any evidence against it in this respect. This,
strength may be related to the fact that the representation is claimed to be
representative.
Discussion
Consider the case where there is a simulation where there
are elements that are unrepresentative (unconstrained by information
from knowledge about the workings of the target domain) yet where minor changes
in these elements (i.e. changes that are still consistent with that knowledge)
significantly change the representative outcomes. In this case, in what
way can the simulation be said to usefully inform us about its target social
phenomena?
Consider the various ways in which one could try to use a
simulation in such a case:
1.
To predict something about the observed outcomes from the simulation
outcomes. This would depend upon being able to identify that the set-up of
the simulation is the one relevant to the observed so that one can the
corresponding outcome can be obtained from the simulation. However this is not
possible since we do not know which set-up is the right one since they are not
determinable using information from the target phenomena.
2.
To explain something about the working of the mechanisms in what is
observed from the unfolding of the mechanisms in the simulation. This
would depend on there being a strong relation between the unfolding of the
process in the simulation and that in the target phenomena. However, in this
case we have no reliable reason to suppose that this is the case (even if the
significant outcomes are the same). It could be that the flexibility we have
in choosing the mechanism is enough to allow us to (inadvertently) ‘fit’ the
outcomes.
3.
To reverse engineer something about the underlying mechanism (what
corresponds to the set-up in the simulation) from what outcomes are observed to
occur in the phenomena. This would depend upon being able to tell that the
class of mechanisms that produce a known outcome, where all other necessary
parts of the simulation set-up being determined from knowledge about the
target. This is possible (albeit unlikely in the extreme) if there were no
parts of the necessary mechanism that were not representational and something
like the envelope of possibilities left were checkable.
4.
To establish the behaviour of a class of models (a sort of ersatz
maths). This is easy to do in the sense that any time one runs a
simulation one establishes something about the relation between set-up
and outcomes is established. However to do this in a way which is at all
useful to others is quite difficult. In particular, if others are to be able
to use the results the necessary core (and corresponding significant aspects of
the results) has to be sufficiently reliable, clear and general. Usually
authors do not try to justify their simulations solely on this basis (due to
its difficulty), but rather fudge the issue by also relying on some weak but
vaguely defined relevance to social phenomena.
Conclusion
Using floating point numbers for things in simulation
models is easy – the apparently simple, quick way of getting things working. It
is also attractive in that there is a wide range of mathematical analytic and
statistical techniques that can be brought to bear. However, numbers (and
especially floating point numbers) are deceptively tricky things. They have all
sorts of counterintuitive properties, which in particular circumstances can
reveal themselves in model outcomes. Whilst there are technical solutions that
can help avoid these traps (Polhill, Izquierdo and Gotts 2005), the only way to
truly avoid such "model artefacts" is to implement (i.e. model) the
processes in one’s model in a causally and descriptively adequate manner. Then
any unexpected results that are obtained may be checked (at least in a rough
qualitative way) with what is observed.
Acknowledgements
Thanks to all those with whom I have discussed and
developed these ideas over the years, including: Scott Moss, David Hales,
Juliet Rouchier, Luis Izquierdo, Gary Pohill, Guillaume Deffuant, Frederick
Amblard, Rosaria Conte, Nigel Gilbert, Matt Hare, Anne van der Veen, Rodolfo de
Sousa, and Olivier Barthelemy.
Bibliography
Deffuant, G., Amblard, F. and Weisbuch, G. 2004, “Modelling
Group Opinion Shift to Extreme: the Smooth Bounded Confidence Model”. Proceedings
of the European Social Simulation Association Conference, 2004, Valladolid,
Spain.
Deffuant, G., Amblard, F., Weisbuch, G. and Faure, T.
2002, “How can extremism prevail? A study based on the relative agreement
interaction model”. Journal of Artificial Societies and Social Simulation,
5(4) http://jasss.soc.surrey.ac.uk/5/4/1.html
Edmonds, B. 2000, “Commentary on ‘A Bargaining Model
to Simulate Negotiations between Water Users’ by Sophie Thoyer, Sylvie
Morardet, Patrick Rio, Leo Simon, Rachel Goodhue and Gordon Rausser”, Journal
of Artificial Societies and Social Simulation, 4(2).
http://jasss.soc.surrey.ac.uk/4/2/6.1.html
Edmonds, B. 2001, “The Use of Models - making MABS
actually work”. In. Moss, S. and Davidsson, P. eds., Multi Agent Based
Simulation, Springer: Lecture Notes in Artificial Intelligence, 1979,
pp.15-32.
Edmonds, B. and Moss, S. 2001, “The Importance of
Representing Cognitive Processes in Multi-Agent Models”. In: Dorffner, G.,
Bischof, H. and Hornik, K. eds., Proceedings of the International Conference
on Artificial Neural Networks ICANN’2001 August 2001, Vienna, Austria.
Springer: Lecture Notes in Computer Science, 2130, pp.759-766.
Edmonds, B. 2004, “Against the inappropriate use of
numerical representation in social simulation”. CPM Report 04-131, MMU.
http://cfpm.org/cpmrep129.html
Edmonds, B. 2004, “The Emergence of Symbiotic Groups
Resulting From Skill-Differentiation and Tags”. Proceedings of the AISB 2005
Symposium on Socially-Inspired Computing day on Emerging Artificial Societies.
University of Herts. April 2005, UK. http://cfpm.org/cpmrep140.html.
Edmonds, B. and Moss, S. 2005, “From KISS to KIDS – an
‘anti-simplistic’ modelling approach”. In P. Davidsson et al. Eds.: Multi
Agent Based Simulation III. Springer, Lecture Notes in Artificial
Intelligence, 3415, pp.130–144. http://cfpm.org/cpmrep132.html
Edmonds. B. and Hales, D. 2004 “When and Why Does
Haggling Occur? Some suggestions from a qualitative but computational
simulation of negotiation”. Journal of Artificial Societies and Social
Simulation, 7(2) http://jasss.soc.surrey.ac.uk/7/2/9.html
Hemelrijk, C. 2000, “Sexual attraction and
inter-sexual dominance among virtual agents”. In Moss, S. and Davidsson, P.
eds. Multi-Agent Based Simulation, Springer: Lecture Notes in
Artificial Intelligence, 1979, pp.167-180.
Hemelrijk, C. 2003, “Social phenomena emerging by
self-organisation in a competitive, virtual world (“DomWorld”). Proceedings
of the European Social Simaulation Association, Gronigen, the Netherlands,
2003.
Holland, J. 1993, “The Effect of Labels Tags on Social
Interactions”. SFI Working Paper 93-10-064. Santa Fe Institute, Santa Fe, NM.
http://www.santafe.edu/sfi/publications/wplist/1993
Moss, S. and Edmonds, B. 2005, “Sociology and
Simulation: - Statistical and Qualitative Cross-Validation”, American
Journal of Sociology, 1104, pp.1095-1131.
Polhill, J. G., Izquierdo, L. R. and Gotts, N. M. 2005,
“The Ghost in the Model and Other Effects of Floating Point Arithmetic”, Journal
of Artificial Societies and Social Simulation, 8(1).
http://jasss.soc.surrey.ac.uk/8/1/5.html
Riolo, R. L., Cohen, M. D. and Axelrod, R 2001, “Evolution
of cooperation without reciprocity”. Nature, 411:441-443.
SIGMUND, K. and Nowak, M. A. 2001, Evolution - Tides
of tolerance. Nature 414, pp.403.
Stauffer, D. Sousa, A. and Schulze, C. 2004 “Discretized
Opinion Dynamics of The Deffuant Model on Scale-Free Networks”. Journal of
Artificial Societies and Social Simulation, 7(3).
http://jasss.soc.surrey.ac.uk/7/3/7.html
Thoyer, S et al. 2000, “A Bargaining Model to Simulate
Negotiations between Water Users”. Journal of Artificial Societies and
Social Simulation, 4(2). http://jasss.soc.surrey.ac.uk/4/2/6.html
Author biographies
Bruce Edmonds is a Senior Research Fellow at the
Centre for Policy Modelling. For more about the CPM see http://cfpm.org, for more about him and his
publications see http://bruce.edmonds.name.
