Artificial Science
– a simulation test-bed for
studying the social processes of science
Centre for Policy
Modelling
Manchester Metropolitan University
cfpm.org/~bruce
1 Introduction
Science is important, not
only in the knowledge (and hence power) it gives humans, but also as an example
of effective distributed problem solving that results in complex and compound
solutions. For even though it is usual
for one or two individuals to be credited for any particular discovery in
science, their efforts almost always use a host of results and techniques
developed by other scientists. In this
sense all scientists "stand on the shoulders of giants" in order to
"see a little further". Thus,
contrary to the architypal image of lone geniuses labouring to prove their
ideas despite the opinions of thier colleagues, science is fundermentally a
social activity. A collection of
individuals, however gifted, that did not communicate would not be able to
develop science as we know it. Even the
earliest scientists such as Galileo were building on the ideas of others
(Copernicus) and using the technology produced by others (the telescope). Indeed some philosophers (e.g. [18]) have claimed that the only things that distinguishes
the process of science from other social processes are its social norms and
processes.
These processes become
the more remarkable, the more they are examined. It turns out that science manages to implement many features that
have been difficult to achieve in distributed AI and multi-agent systems. These include: the spontaneous
specialisation and distribution of skills accross the problem space; the
combination of advances and results from many different individuals to form
complex chains of inference and problem solving; the reliability of estabished
results in comparison to the uncertain reliability of individuals' work; the
spontaneous autopoesis and self-organisation of fields and sub-fields,
continually adapting to problems and degrees of success; the ability of science
(as a whole) to combine "normal science", characterised by much
cooperative work within a common framework and "revolutionary
science" characterised by sharp competition between individuals and
frameworks; and the ability of science to produce coherent developments of
knowledge whilst, at the same time, maintaining variety and criticism so that
it can quickly adapt to the failure of any particular developments. All of this is achieved with a relative lack
of: explicit central coordination; use of market mechanisms; global and
explicit agreement about norms or methods; or well-defined hierarchies.
Thus science is an
important subject for study in its own right, and thus also its critical social
processes. The question is not so much
that it is worth modelling, but how one approach modelling it in a useful
way. It is the aim of this paper to
suggest a framework for a set of investigations that will advance such a
project. Thus the framework will be
described as well as a first implemented instantation of the framework. Although it is the framework which I
consider more important, the exhibited simulation exhibits results that are
interesting in their own right.
Traditionally there is
the ‘building-block’ picture of science [11] where knowledge is slowly built up, brick by brick,
as a result of reliable contributions to knowledge – each contribution standing
upon its predecessors. Here, as long as
each contribution is checked as completely
reliable, the process can continue until an indefinitely high edifice of
interdependent knowledge has been constructed.
However other pictures have been proposed. Kuhn in [14] suggested that often science progresses not gradually
but in revolutions, where past structures are torn down and completely new ones
built.
Despite the importance
of the social processes in science to society, they are relatively little
studied. The philosophy of science has
debated, at some length, the epistemological aspects of science – how knowledge
is created and checked ‘at the coal face of the individual’. Social processes have been introduced mainly
by critics of science – to point out that because science progresses through
social processes it is ‘only’ a social
construction, and thus has no special status or unique reliability.
Here I take a neutral
view – namely, that it is likely that there are many different social processes
occurring in different parts of science and at different times, and that these
processes will impact upon the nature, quality and quantity of the knowledge
that is produced in a multitude of ways and to different extents. It seems clear to me that sometimes the
social processes act to increase the reliability of knowledge (such as when
there is a tradition of independently reproducing experiments) but sometimes
does the opposite (when a closed clique act to perpetuate itself by reducing
opportunity for criticism). Simulation can perform a valuable role here by
providing and refining possible linkages between the kinds of social processes
and its results in terms of knowledge.
Earlier simulations of this sort include Gilbert et al. in [10]. The
simulation described herein aims to progress this work with a more structural
and descriptive approach, that relates what is done by individuals and journals
and what collectively results in terms of the overall process.
2 The Simulation
2.1 Motivation and Related Work
The aim of this simulation
is to suggest a set-up within which the social/interactive aspects of
collective knowledge discovery can be explored. It therefore contrasts with attempts to understand what a single
scientist does, by modelling and philosophy.
Computational models of aspects of the work of a single scientist include
those of problem solving [21] and induction [12]. Implemented
models which attempt to synthesise the essential processes of a single
scientist more as a whole include BACON [17], Meta-DENDRAL [1] and PI [24] (this last providing the best general discussion on
the project of computationally modelling science).
There is a similar
tendancy in the philosophy of science, with a historical concentration on what
a single scientist does. Social aspects
of science have been brought in mainly as a critique of the “received picture”
of science [11] – the argument is roughly that because social processes
are involved in the construction of scientific theories, that scientific truths
do not correspond to an objective truth.
The philosophy of
science has moved from a priori
normative accounts (how science should
work) to a postiori descriptive accounts,
largely due to Kuhn’s account of how revolutions (“paradigm shifts”) occur in
science [14]. The exact
nature of the social processes that occur in science are not, in general,
condsidered. Exceptions include:
Tolmin’s book [25], a recent paper by Giere [9] and a book by Knorr-Cetina [13]. However,
these processes are even more rarely modelled – the only exception I know that
touches on this being [10].
The individual agents
in the specific simulation below are fairly simple compared to some of the
models listed above – I have concentrated instead on the flow of information
between agents via a publically accessible repository (corresponding to a
journal) and how the agents select what knowledge to learn and use. This does not mean that a model with more
sophisticated and realistic agents would not be better, just that I have not
done this.
2.2 The General Structure
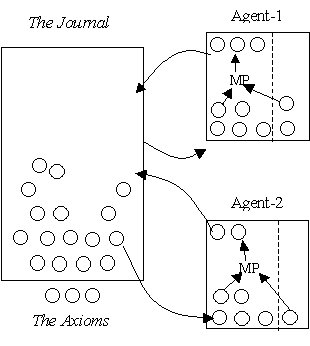
Figure 1. An illustration of the set-up with two agents
(circles are items of knowledge, rectangles are agents)
The simulation involves a
fixed number of agents (representing individual or closely collaborating teams
of scientists) a journal (only one in the present simulation) which includes
the set of formal sentences representing the knowledge that is discovered and
published. Each agent has a private
store of knowledge which may or may not be public (i.e. an axiom or published)
– this store is their working knowledge.
To use a public item of knowledge this must be added to their private
store before they can use it to produce new items. They submit some of this to the journal which selects (according
to some criteria) a subset which is then published and becomes available to
others. The whole set-up is
illustrated in Figure 1.
2.3 The Environment and Task
Science continually
progresses into the unknown. In science
sometimes the end points are known – for example, when it is known that a
certain disease is passed on genetically, then the genes that are responsible
may be sought. Often, however,
scientific discoveries are a surprise to their discoverers. Thus it is often the case that scientists do
not know exactly what it is they are searching for. This is in contrast to engineering where it is usual to know the
problem for which an answer is sought. This poses a problem for a would-be simulator
of the social and cognitive processes that contribute to science – how can one simulate creative discovery of
the unknown?
The answer I have
chosen is to use a formal system (logic) as the representation of knowledge, so
that the agents work on the logical structures to produce new structures
(theorems in the logical sense), but where it is impossible to know in advance
how useful these will be. This decision has distinct consequences both in terms
of the possibilities and limitations of the model and in terms of the
assumptions on which it relies. These
will be discussed later. This can be
seen as following [17].
Thus the universe of
knowledge that the agents will explore in this simulation is the set of
inferable formal sentences derivable from a given set of initial axioms. For ease of implementation I have restricted
my self to logics formalisable as Hilbert Systems (that is, ones with a set of
axioms and a single rule of inference, Modus Ponens, which is recursively applied,
see an introduction to logic, e.g. [4]). The agents
can produce new sentences by applying existing sentences to other sentences
using Modus Ponens (MP). The form of
this is if you know ![]() and you know
and you know ![]() then you can also conclude
then you can also conclude ![]() (written
(written ![]() ). An example of this
is: when
). An example of this
is: when ![]() is
is ![]() and
and ![]() is
is ![]() : from
: from ![]() and
and ![]() we can infer
we can infer ![]() . This is illustrated
in Figure 2.
. This is illustrated
in Figure 2.
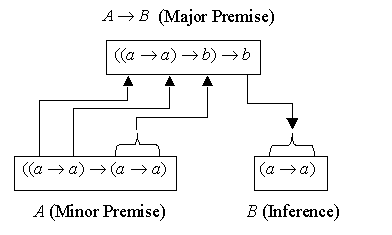
Figure 2. An illustration of the working of MP
The agents
thus have the task of discovering new formal sentences. The advantages of this structure are that:
(1) future developments from any item of knowledge are not known in advance;
(2) knowledge is not only useful as an end in itself but can be used as a tool, acting upon other knowledge to
produce new knowledge (as the major premise in MP, the A in Figure 2);
(3) the programmer of the simulation does not necessarily know how one gets to any given theorem of the
system, which reduces the temptation to bias the simulation to get specific
results; (4) the task is suitably hard,
as the development of automatic theorem-provers shows.
In order to
set up the field of knowledge that the agents will collectively explore the
simulator needs to list the symbols being used and list the axioms of the
relevant logic. Optionally the
simulator can also list a number of known theorems that are considered
important by logicians and give them a value, though how one derives these is not needed to be specified (this is for
the agents to find out). These ‘target
theorems’ are unknown to the agents until they discover them. They represent (in the loosest possible way)
useful technologies that may come out of science. Counting how many of these have been discovered (and the total
value of their ‘worth’) is an indication of the effectiveness of the collective
discover effort, and can be a better measure that simply counting how many new
sentences have been discovered since it is easy to develop trivial elaborations
of already known sentences.
2.4 The Agents
In this simulation the
agents have a very simple-minded approach to the production of new knowledge:
agents select two items in its own store of knowledge and apply the MP rule to
it, which may or may not result in a new item of knowledge which is added to
their store. Each agent has two private
stores of knowledge: firstly, a store
of formal sentences that are candidates as the minor premises for the MP rule
and secondly, store composed of
candidates for the major premises. The
former roughly corresponds to the primary knowledge of a scientist and the
second as the set of techniques of the agent since it determines which
transformations can be applied to which items and what can be produced.
Each time period the
agent does the following:
1. Decide what new items of knowledge (both major
and minor) to add to its private store from the published set, also which to
drop.
2. Decide which major premise and what set of
minor premises it will try with the MP rule and add any results to its (minor)
store.
3. Decide which of its private knowledge (that is
not already public) it will submit to the journal.
There are obviously
many different ways of making these decisions.
Each of these ways will have a (varying) impact upon the development of
the collective knowledge. In addition
to the above, gradual, update policy if the agent fails to discover any new
sentences during a given number of consecutive time periods it may ‘panic’ and
completely replace one of its stores with a new set of sentences.
Key parameters and setting
of the agent are as follows. For each
of its private knowledge stores (minor and major) the update policy includes
the following: its size; the rate at which it adds or drops knowledge from this
store; how it does either the
addition; the dropping; or the panic replacement (at random/probabilistically
the best/the best judge either on raw past fertility or past fertility with a
bias towards simplicity); whether it panics and how long it endures lack of
success before panicking; which to try (the best/probabilistically the
best/untried/random); and how it judges what it knows (personal fertility/lack
of failure to produce new knowledge). Also its submission policy: whether it
submits all novel (i.e. unpublished) sentences to the journal or only the simplest/best
ones.
2.5 The Journal
The journal (the Journal of Artificial Sentences and
Successful Syllogisms) is the gatekeeper to the repository of public
knowledge. The key aspect of the
journal is the criteria it uses for assessing the items submitted to it, so as
to decided what (if any) it will publish.
This occurs in three basic stages: the short-listing of those that met
basic criteria; the evaluation of those short listed; and their ranking. The journal then published a selection of
the top n in the ranking (if there
were more than n short listed),
otherwise all of them. This final
selection could be the best (from the top); probabilistically on the weighted
score (the higher the score the more likely it is to be selected); randomly or
simply all of them. The evaluation of
the submissions was done as a weighted sum of scores for a number of aspects:
the number of variables in the sentence, its brevity, the extent to which it
shortens sentences when used in MP, and the past success of the author. The weights and selection policies can be
set by the programmer.
2.6 Methods of evaluation
Key to many of the decisions
made by the agents or the journal is the evaluation of the existing
knowledge. Ultimately this can be
considered as a guess at the future usefulness of that knowledge, in terms of
either: its productivity in producing new knowledge; reaching the hidden
‘target theorems’; or in getting published.
This may be done in a number of ways.
One way is by looking at the historical record of how productive the
sentence has been in the past in resulting in new published knowledge (this can
be done in a recursive way to value sentences that have produced productive
sentences etc.). Another way is to look
at the most published agents and see what knowledge they have used (in
published work). Other ways include
considering features of the sentences themselves, for example measures of their
simplicity (how many variables they have, how long they are, to what extent the
sentence results in a shortening of sentences when applied using MP, etc.)
3 Preliminary Results
At the time of writing only
preliminary results are available, which explore only a very small proportion
of the possibilities inherent in this model.
Many of the settings
do affect the outcomes to a significant degree. However many which increase the short-term success (measured in a
number of different ways) of the scientific progress also have the effect of
reducing the longer-term maintenance of new results. Thus, for example, adding new sentences at random to an agent’s private knowledge (i.e. regardless of the
agent’s evaluation of sentences) decreased the short-term level of discovery
markedly, but then that level of discovery lasted a longer time. In contrast where agents follow other agents
closely (preferentially adding sentences used successfully by others) results
followed much more quickly to begin with but then petered out to zero after
40-60 time periods (only then deviating from zero when an agent panicked and
hit lucky with its new set of knowledge).
Such a result would indicate that a process of fairly frequent, but
collective revolution was one of the most efficient collective modes of
discovery.
In general most of the
targeted sentences were either discovered very soon, or never. This suggests that “deep” sentences (those
difficult to reach in this collective but individually stupid manner) require
guidance from a deeper knowledge of the individual logics concerned, and is not
so amenable to a generic approach (collective or otherwise).
3.1 Varying the rate of publication
The set of results I will
exhibit here are those concerning the effect of the journal’s policy on the
whole discovery enterprise. The number
selected by the journal to publish were varied from the set {1, 2, 3,…,10} in
250 independent runs with 20 agents and 50 iterations. The journal selected according to a number
of factors, which were (in order of importance): the extent to which a formula
had the effect of shortening formula when applied as the major premis in MP;
the shortness of the formula itself; the past publishing success of the author;
and the fewness of the number of distinct variables in the formula. The journal
ranks all submissions according to a score composed of a weighted sum
representing the former priorities.
Agents submit all formula they discover to the journal if they have not
been previously published. Each agent
has a store of 4 major premises and 27 minor premises and tries 9 different
combinations of major and minor premises with MP each iteration. Generally
agents change 1 major and 2 minor premises each time. New major premises are chosen probibilistically according to a
formula’s past fertility in producing formula that are published. Minor premises are chosen at random. If an agent is completely unsuccessful for a
certain length of time they panic and replace all of their premises with new
ones. The exact settings are those
listed in section 6.1 in the appendix, and were those found in unstructured
experimentation to be one of the more productive settings for agent behaviour.
The journal was never
short of material to publish even when it was publishing 10 formulae each
iteration. Thus the rate of publishing
is directly related to the size of the body of publically known formula
accessible to agents, as is shown in Figure 3.
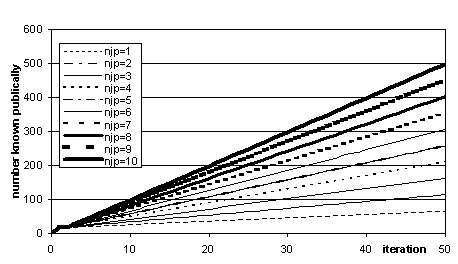
Figure 3. Total number of formulas publically known at each iteration (averaged over 25 runs) for different journal publication rates (njp)
However, this does not mean that a higher publication rate results in finding more useful knowledge, for this does not tell us how useful these are. The system was given a list of 110 target theorems – those listed as significant in logic textbooks. Figure 4 shows the average number of these theorems that the system discovers for different publication rates (averaged over 25 runs). The publication rate did not make a big difference to the number of discovered targets and that almost all discovery occurred early on. Usually 11-12 targets were found. Only once 20 were found at publication rate of 2 (this explains why this line is higher than the others).
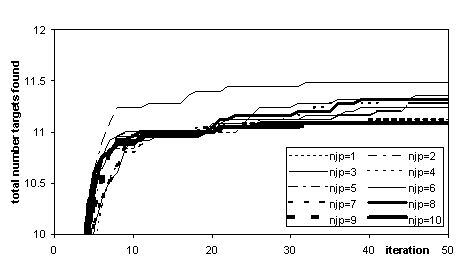
Figure 4. Total number of target formulas discovered (averaged over 25 runs) for different journal publication rates (njp)
What is interesting is that this discovery rate was fairly independent of the number of submissions to the journal. Roughly, the higher the publication rate, the lower the number of submissions as Figure 5 shows. Whilst at first sight this seems counter-intuitive, it is less so given that the more knowledge has been published, the more difficult it is to find something new to submit. Although in each case the system did learn to find very many of the target formulae. Clearly, in this particular case, published knowledge was not so useful in producing new kinds of knowledge.
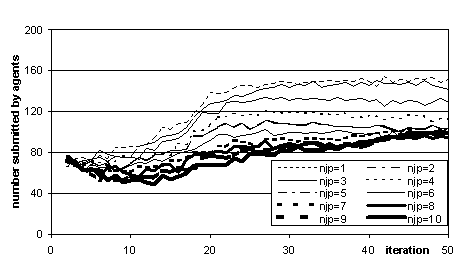
Figure 5. Total number of formulas submitted at each iteration (averaged over 25 runs) for different journal publication rates (njp)
Also interesting is the disparity between agents in terms of the number of new formula discovered (i.e. unpublished and not known by the agent concerned). Whilst initially a higher publication rate meant less disparity between agents, after a while some agents learnt to do so much better than others and dominate (Figure 6).
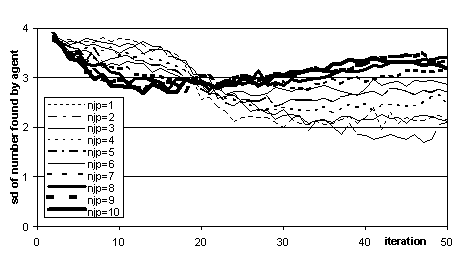
Figure 6. Spread (standard deviation) of the number of unpublished formula found by agents each iteration (averaged over 25 runs) for different journal publication rates (njp)
Now to look at a particular run (the one which discovered 20 formulae). Figure 7 shows the number discovered the 20 agents – the thickness of each band represents the number that agent found. Note the variation in terms consistency in performance.
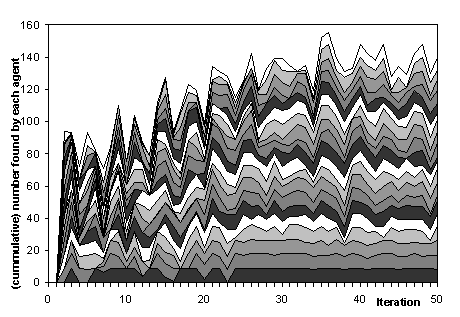
Figure 7. The number of unpublished formula found by each agent in a single run (each agent is represented by a single ‘band’ in the chart, the best on average at the bottom)
Figure 8 shows the average and the standard deviation of the number discovered by each agent in the same run as above. The number generally increases, and the standard deviation (in terms of raw discovery) tends to increase. It may be that the initial diversity facilitated the early, relatively high target discovery rate.
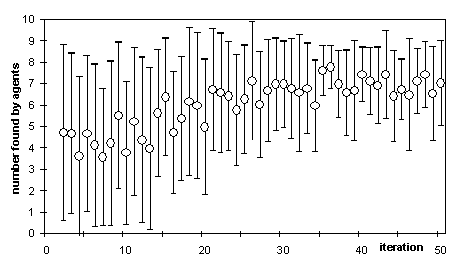
Figure 8. The average number of unpublished formula found by each agent in the particular run (average is show by the circles and the vertical lines show +/- one standard deviation)
The purpose of these
results is not to conclusively show
anything in particular about how many papers a real journal should publish, or
even how many might be optimal. Rather
it is to show how such a set-up can illuminate and explore such questions.
4 Discussion
4.1 The Possibility of Limited Validation
Following [10], it may be possible to compare the structure of the
published knowledge that results in this simulation (i.e. which authors/items
are derived from which previous items by which authors) might be compared with
the structure found in citation indexes such ISI using a number of measures,
statistics or structural comparisons.
Unfortunately negotiations with ISI indicate that they are only prepared
to part with the structural information of their databases (suitably
anonymised) for rather large quantities of money (i.e. around $30000). If anyone knows of an alternative source,
please contact the author.
4.2 Limitation and Extensions
Clearly many of the
limitations in this simulation are arbitrary:
Thus I list a few possible extensions as examples:
·
decision methods
of arbitrary complexity can be implemented in agents (indeed these methods
could themselves be evolved by GP) – in particular they might do more reasoning
about causality [22];
·
there could be
many journals so that the: prestige of a journal; its topics; its impacts and
the quality of its submissions could be allowed to co-develop inside the
simulation;
·
instead of
inferring new knowledge the agents could hypothesise and test candidate
sentences performing tests on the logical semantics (e.g. a row of the truth
tables in classical logic) – this would introduce levels of uncertainty as to
the reliability of any particular item of knowledge;
·
a peer review
system could be implemented whereby reviewers are selected depending on their
past publishing success and impact; they could use their own experience of what
is useful as their criteria for judging entries and their own tests; and items
could be selected resulting on the votes of reviewers;
·
informal social
networks could be introduce to pass knowledge from agent to agent other than
via official journals;
·
agents should be
allowed to reproduce in terms of the students they teach and retire after a
suitable time (or if they are spectacularly unsuccessful).
More fundamentally the present structure of the simulation assumes that
there is some independent ‘correct’
knowledge to be discovered and that it is checkable. This could be corrected by providing some database of atomic
facts (e.g. the linkage structure of part of the web) and then hypotheses about
these could be attempted to be induced (as in inductive data-mining
techniques). The journal (or journals)
would not be able to 100% check the veracity of any knowledge but have to rely
on some fallible process to come to a judgement upon the knowledge. However, a disadvantage of such an approach
is that it would lack the tight inter-dependency of knowledge that seems to be
such a characteristic of some sciences[1].
4.3 Relationship with Distributed Theorem Proving
(DTP)
The simulation is a forward-chaining theorem prover,
and can be seen as an answer to [8] since it could be truly distributed. However it is a very inefficient one – it is
deliberately generic in that it has
not been ‘tuned’ for performance (by using deep properties of the particular
logic being investigated), since this is not its goal. Despite this, lessons learned in this
simulation do have potential in terms of informing the design of distributed
theorem provers and vice versa from
what is discovered about efficient DTP to this simulation (and potentially
science itself[2]).
OTTER [26], a particular and quite successful theorem prover is
quite close to the how a single agent works in the above simulation. It has a list of candidate minor and major premises
and works on these to extend the set of known sentences until it reaches the
target theorems. It allows for a large
range of techniques in re-writing formulas, guiding search and applying rules
that are not touched upon here.
4.4 Key Questions and Issues
Perhaps most the important
aspect of this paper is that it shows how a host of important issues and
questions concerning the social processes of science (and science-like
processes) may be investigated. Is
Feyerabend’s thesis that any imposed method for constructing scientific
hypotheses is counterproductive [7], and the best way forward is “anything goes”? To what extent does the particular formal
system affect the progress in any particular field [5]. In what
circumstances and in what ways can inter-scientist processes contribute to the
reliability (or otherwise) of the knowledge produced [9]? Is it
helpful to have an inviolate core of unquestioned truths and techniques in a
field or is it better that everything is open to revision [15]? Do
scientists, in effect, create blind variations to then be tested as suggested
in [2]? Are
scientific norms the key characteristic that distinguishes science from other
human institutions [19]? When is it better to use a simplicity bias in the
search for useful knowledge [6]? Answers to
these questions may be suggested in functional terms by studying simulation
models on the lines of the one discussed.
4.5 Conclusion
I hope to have shown how it
is possible to capture some aspects of the social processes that contribute to
the construction of science. Such
modelling has the potential to intermediate between observations concerning how
science works and areas of distributed knowledge discovery in computer science,
e.g. automated theorem proving. It could help sort out the roles of the
different processes in science confirming or disconfirming philosophical
speculations as well as provide productive ways to parallelise computational
tasks such as theorem proving.
5 References
[4]
Copi (1982) Introduction to Logic. New York:
Macmillan.
[7]
Feyerabend, P.
(1965) Against Method. London: New Left Books.
[9]
Giere, R. (2002)
Scientific cognition as distributed cognition. In [3], pp. 285-299.
[10] Gilbert, N. (1997) A simulation of the
structure of academic science. SociologicalResearch
Online, 2(2), http://www.socresonline.org.uk/2/2/3.html
[11]
Hempel, C. G.
(1966) Philosophy of Natural Science.
Englewood Cliffs, N.J. :Prentice-Hall.
[18]
Longino, H.
(1990) Science as Social Knowledge. Princeton: Princeton University Press.
[20] Moss, S., Edmonds, B. and Gaylard, H.(1996)
Modeling R&D strategy as a network search problem. Workshop on The Multiple
Linkages between Technological Change, Human Capital and the Economy,
University "Tor Vergata" of Rome, March 1996. (http://cfpm.org/cpmrep11.html)
[21]
Newell, A. and
Simon, H. A. (1972) Human Problem Solving. Englewood Cliffs, NJ: Prentice-hall.
[22]
Pearl, J. (2000) Causality. Oxford University Press.
[23] Popper, K. (1965) Conjectures and Refutations.
New York: Basic Books.
[24]
Thagard, P.
(1988) Computational Philosophy of
Science. MIT Press.
6 Appendix
6.1
Parameter
settings
addRateMajor = 1
dropRateMajor = 1
addRateMinor = 2
dropRateMinor = 2
numInitialSAgents =
20
maxIteration = 50
maxRun = 250
numMajor = 4
numMinor = 27
interalScoreDecay =
0.9
fertilityDecay = 0.9
numToTry = 9
panicSoonTime = 4
panicLaterTime = 12
maxNumberToPublish =
[1,…10]
minNumberOfVariablesForPublication
= 1
shorteningWeight = 0.1
shortnessWeight = 0.01
sourceWeight = 0.001
numVariablesWeight = 0.0001
modelBehaviourList =
[fertilityIsInverseLength matchTargetGenerically publishBest]
behaviourList =
[submitAll]
majorBehaviourList =
[addFertileProb dropWorst feedbackOnUsedFailure panicLater replaceBestIfBad
tryBest]
minorBehaviourList =
[addRandom dropWorstProb feedbackOnFertility panicSoon replaceProbFertileIfBad
tryUntried]
6.2 Sample output from selected run
Iteration 1
Iteration 2
agent 2 found
'->' A ('->' A ('->' A A))
agent 2 found '->' ('->' A B) ('->' ('->' C B) ('->' A ('->'
C B)))
agent 2 found '->' ('->' A B) ('->' ('->' B A) ('->' B A))
agent 2 found '->' ('->' A B) ('->' ('->' A B) ('->' A B))
agent 2 found '->' ('->' A A) ('->' A A)
agent 2 found '->' ('->' A A) ('->' ('->' A A) ('->' A A))
agent 6 found '->' A A
agent 6 found '->' ('->' A A) ('->' A A)
agent 10 found '->' ('->' A A) ('->' A A)
agent 12 found '->' A ('->' A ('->' A A))
agent 12 found '->' ('->' A B) ('->' ('->' C B) ('->' A ('->'
C B)))
agent 12 found '->' ('->' A B) ('->' ('->' B A) ('->' B A))
agent 12 found '->' ('->' A B) ('->' ('->' A B) ('->' A B))
agent 12 found '->' ('->' A A) ('->' A A)
agent 12 found '->' ('->' A A) ('->' ('->' A A) ('->' A A))
agent 18 found '->' ('->' A A) ('->' A A)
agent 19 found v A ('¬' A)
agent 19 found '->' ('->' A B) ('->' ('->' B C) ('->' A C))
agent 19 found '->' ('->' A A) ('->' ('->' A A) ('->' A A))
agent 19 found '<->' ('&' A ('¬' A)) F
Iteration 3
agent 3 found
'->' ('->' A ('->' B C)) ('->' B ('->' A C))
agent 3 found '->' ('->' A ('->' ('->' B C) D)) ('->' ('->' B
C) ('->' A D))
agent 6 found '->' ('->' A ('->' B B)) ('->' A ('->' A ('->'
B B)))
agent 6 found '->' ('->' A ('->' A B)) ('->' A B)
agent 6 found '->' ('->' A B) ('->' ('->' B A) ('->' A B))
agent 17 found '->' ('->' A ('->' A B)) ('->' A B)
agent 19 found '->' ('->' A B) ('->' ('->' C A) ('->' C B))
agent 19 found '->' ('->' A B) ('->' ('->' C ('->' ('->' A B)
D)) ('->' C D))
Iteration 4
agent 7 found
'->' ('->' A B) ('->' ('->' ('->' A B) C) C)
agent 7 found '->' A ('->' ('->' A B) B)
agent 13 found '->' ('->' A ('¬' A)) ('¬' A)
agent 15 found '->' ('->' A ('¬' A)) ('¬' A)
Iteration 5
Iteration 6
Etc.