Against the inappropriate use of numerical representation in social simulation
Bruce Edmonds
Centre for Policy Modelling,
Manchester Metropolitan University
cfpm.org/~bruce
“To a man with a hammer every screw looks like a nail” (Trad.)
Introduction: what’s wrong with numbers?
All tools have their advantages and disadvantages and for all tools there are times when they are appropriate and times when they are not. Formal tools are no exception to this and systems of numbers are examples of such formal tools. Thus there will be occasions where using a number to represent something is helpful and times where it is not. To use a tool well one needs to understand that tool and, in particular, when it may be inadvisable to use it and what its weaknesses are.
However we are in an age that it obsessed by numbers. Governments spend large amounts of money training its citizens in how to use numbers and their declarative abstractions (graphs, algebra etc.) We are surrounded by numbers every day in: the news, whether forecasts, our speedometers and our bank balance. We are used to using numbers in loose, almost “conversational” ways – as with such concepts as the rate of inflation and our own “IQ”. Numbers have become so famliar that we no more worry about when and why we use them than we do about natural language. We have lost the warning bells in our head that remind us that we may be using numbers inappropriately. They have entered (and sometimes dominate) our language of thought. Computers have exasperbated this trend by making numbers very much easier to store/manipulate/communicate and more seductive by making possible attractive pictures and animations of their patterns. More subtley, when thought of as calculating machines that can play games with us and simulate the detail of physical systems, they suggest that everything comes down to numbers.
For this reason it is second nature for us to use numbers in our social simulations and we frequently do so without considering the consequences of this choice. This paper is simply a reminder about numbers: a call to remember that they are just another (formal) tool; it recaps some of the conditions which indicate when a number is applicable and when it might be misleading; it looks at some of the dangers and pitfalls of using numbers; it considers some examples of the use of numbers; and it points out that we now have some viable alternatives to numbers that are not any less formal but which may be often preferable.
So, to be absolutely clear, I am not against numbers per se, merely against their thoughless and inappropriate use. Numbers are undeniably extremely useful for many purposes, including as language of thought – just not for every purpose and in every domain. Also, to be absolutely clear, I do not think there is any system of representation that is superior to the others – including: logic; programs; natural language or neural networks – but that different representations will be more useful (and less misleading) in different circumstances and for different purposes. Some of my best friends are numbers.
A little bit of measure theory
There are, of course, different ways of using numbers as representations depending upon what properties of numbers you are using. Some of the possibilities are listed below going from weaker properties to stronger ones. Each possible property has its uses and limitations. They are derived from (Stevens 1946) distinctions of measures into levels or types.
· Unique labelling – an indefinite supply of unique labels is required (as with players in a football team), the only aspect of numbers that is significant is that each label is distinguishable from the others. You can not use comparisons or arithmetic.
· Total order – the numbers are used to indicate the ordering of a set of entities (as with ticket numbers in a queing system). Comparisons can be made at any time to quickly determine which of the labelled items is higher in the order. You can not use arithmetic without the danger changing the order in subtle and unexpected ways – that is any transformation needs to preserve the ordering unless the order of what is being represented has changed.
· Exact value – the value of some properties is given without error (as with money or counting), that is using whole numbers or fractions. This is using numbers to represent essentially discrete phenomena – numbers of things or multiples of exact shares of things. No measurement can be involved because measurement processes inevitabley introduce some level of error. The conservation of the things that are being represented underpins the possible arithmetic operations that may be performed on the numbers and comparisons relate to a one-one matching exercise with what is represented. Arithmentic operations that break the exactness of the calculations (like square roots) generally have no meaning in terms of what is being represented in this case.
· Approximate value – where the number indicates some measurement which involves error (as with temperature or length). These are typically, but not always, continuous properties which are not representable exactly in any finite form. Thus as well as errors introduced by measurement and interpretation processes there are also errors introduced by most artithmetic manipulations. That is, you need to be very careful about the accumulation of error with calculation and comparisons. There are techniques to help with problem, e.g. the use of interval arithmentic (Pohill et al. 2003).
Many problems are caused by people using one kind of numbers appropriate to a particular circumstance (e.g. a Likhart scale) which are then processed as if they were another, e.g. using arithmentic. This is quite a common occurrence since there is a temptation to use the full range of arithmentic possibilities as soon as properties are represented as numbers, regardless of whether these are warrented by the nature of what they represent. One of the reasons for this is that they are all called numbers and it is not possible to tell what sort of numerical properties are relevant just by looking at them.
The exact conditions under which numbers can be used in these different ways were formalised as “Measure Theory” from the 1930’s to the 1970’s in the philosophy of science. An introduction to measure theory is (Sarle 1997) and the definitive set of works is considered to be (Krantz et al 1971, Suppes et al 1989, Luce et al 1990).
Some specific difficulties with numbers
In this section I review some of the difficulties that can be associated with the careless and/or inappropriate use of numbers. These difficulties are all, to different extents, avoidable either through careful technique; practice; or the use of alternatives. In the former case the difficulties can be interpreted as simply being due to a sloppy use of numbers, but in the later the mistake lies in trying to use numbers rather than a more appropriate alternative. In many circumstances all forms of representation have their own difficulties, but in all cases it is preferable to be able to choose the best representation for a purpose and to be aware of (and check for) the possible difficulties that result from one’s choice.
Distorting the phenomena
The first and foremost difficulty is when representing something by a number unnecessarily so that it critically distorts the relevant aspects of the target phenomena. Sometimes this seems unavoidable, but surprisingly often it is due to unthinking imitation of what other researchers have done. The most frequent case seems to be when something that is essentially qualitative in nature is represented by an arithmetic number.
This is highlighted by a case where the difference between qualitative and quantitative is very clear: variety. To see why variety might not be numerically representalbe, consider the following case. If one has a set of objects or properties which are satisfactorily representable within a set of numeric dimensions, and one adds a new object or property (that is not well represented by the existing measures) then the new set (which includes the new property) has a greater variety than the old set. Thus variety, in this sense, is not caputurable by any (finite) set of measures. It is distiguished by variation which is simply a measure of how much another measure varies in a set of measurements. Variety in this sense has real operational meaning – for example, when we say that there is a great deal of variety amoung the species in a certain environment this means that it is more likely that some will survive an unexpected catastrophe of a novel kind (such as a totally new predator arriving in the area). If the “variety” was merely a set of different amounts of properties then it would be relatively easy for a new predetor to evolve which would wipe them all out.
Now while it is legitimate to invent post hoc descriptive measures to demonstrate and illustrate an increase in variety that has already occurred, it is another matter entirely to try and implement such an increase in variety via the simple increase along some fixed set of dimensions. The difference is readily apparent if one is co-evolving a set of (possibily artificial) organisms to cope with the change – for the increase along within a fixed set of measures is (eventually) learnable and hence predictable, whereas such surprises such as the appearance of a new predator is not. In the former case it may be possible for some species to learn a strategy that will cope with the change whilst in the later case the only thing that will help (in general) is the variety between species and within species.
Variety of this kind is not directly implementable in terms of any numeric measure of variance (despite the fact that variance might be used as an illustration of the amount of variety). This sort of variety is of a fundermentally qualitative kind. This does not mean that it is not formally implementable at all, simply that it is not well represented in general by a numeric measure (however complicated).
This is not due to deep theoretical differences between the qualitative and the quantitative since all numerical mathematics can be implemented within qualitative set theory and logic (Russell and Whitehead 1962) and vice versa as Gödel showed (1930). Rather it is the practical differences between systems of representation that matter. It is so difficult to represent some kinds of properties within some kinds of system that the practicalities will necessitate that the orginal is distorted in the process (Edmonds 2000).
Similar properties that are not well represented by numbers are examined within the context of the examples in the next section.
Loosing the context
Numbers are very abstract representations, they are the result of abstracting away all the properties except for a single dimension. In particular they do not encode anything about the context in which the abstraction occurred. This brings considerable advantages – one can learn how to manipulate numbers and equations independently of the contexts in which they are applied, so that one can use the learnt formal tool on a wide variety of possible problems. The mainenance of contextual relevance is left up to the humans who use the mathematics – one can not tell this just from the mathematics. Thus the abstract nature of numbers and mathematics allows for possible confusion.
For example, it may be that in a particular simulation each new individual is given a random float in order to provide it with a unique label (it being extremely unlikely that two individuals will have the same float allocated. Later it may be that someone else modifies the simulation so that if two competing individuals happen to have exactly the same fitness then the one with the numerically greater label wins – this seems equivalent to an arbitrary choice since the original labels were randomly generated and it is rare that competing individuals do have exactly the same fitness. However it may be that under certain circumstances life becomes so difficult (or easy) that fitness all reach the same minimum (or maximum), in which case instead of a random set of individuals being selected there will be a bias towards those who happen to have the higher label. Here the orginal intention of unique labels is forgotten and are reused as symmetry breaking mechanism, causing unforseen results. A real example of this kind of confusion is found in (Riolo et al. 2001) where a particular selection mechanism interacts with differences in fitnesses so that the authors misinterpreted a tollerance mechanism as significant when it was not (Edmonds and Hales 2003b).
The semantic complexity of a set of phenomena is the difficulty of formally (i.e. syntactically) modelling that phenomena for a particular purpose (Edmonds 2003). The more semantically complex the target phenomena is, the more important it is to preserve the orginal context of abstraction so the reader may trace back the original meaning of referents in models so as to understand their nature. That does not mean that there is not any possibility of generalisation to other contexts, but it does mean that this needs to be done carefully by knowing the relevant set of properties of what is represented beyond that formally encoded in the model. This issue is discussed more in (Edmonds and Hales 2003a).
The accumulation of error
Approximate numbers are the hardest type of number to use because the traps involved in using them are not easily avoided. Although there are techniques which are very helpful at avoiding these problems there is no technical fix that will always avoid these problems. The nature of the problem is intractable – we are using a finite representation (a float, an interval, an error bound, etc.) for something that can not be finitely represented (an irrational real). Almost any model that uses such finite representations will eventually “drift apart” from what is being modelled with suitabley extreme parameters or when run for a sufficiently long time. Of course, if the system is chaotic the results may diverge quite sharply.
As (Polhill et al 2003) shows, it is not simply that the represented value “drifts” away from the target, but in many cases there is a systematic bias to the drift. This means that simply performing the same run many times using different random number seeds (or slightly different parameter settings) and averaging the results will not avoid the problem. Devices such as “interval arithmetic” (Pohill et al.) may provide assurance (or conversely warnings) in some cases – it would seem particularly useful when there are calculations using floats followed by a comparison which determines subsequent behaviour, but it will not avoid all problems.
More subtle are effects caused by the additional “noise” caused by the continual errors. This is frequently insignificant, but not always. In systems where there are chaotic processes or symmetry breaking is important even small amount of “extra noise” can make a difference.
The creation of artifacts
The distortion of what is being represented, the loss of original context and the inevitable “drift” away from the original phenomena due to approximate representation means that some of the phenomena observed in the resulting process outcomes may well be “artifacts” of the simulation – that is, features of the results that appear qualitatively significant to the modeller but which do not correspond in any way to what is being represented due to the fact that the simulation is working in a way that is different from what the modeller intended.
In a way all complex simulations are full of such artifacts – formal representations (including computer simulations) are always somewhat of a distortion of complex phenomena; and one will rarely understand the complete behaviour of such simulations in all circumstances. However if the modeller has a clear analogy (or mental model) of how the relevant aspects of the simulation should be behaving then this can be compared to the relevant observed behaviour of the model and differences detected. If differences are detected in these significant aspects and there were no bugs at the level of the programming code but a subtle interaction due to the underlying nature of the numeric representation then we may call these effects “artifacts” of the representation.
This is bad news for modellers because it means that they can not be satisfied with simply programming at the level of whatever language or system they are using but have to pay attention to the nature of the representation they are using and its properties. Understandably many modellers react to such problems by wishing them away or ignoring them – “these are simply technical problems and don’t effect my results” seems to be the attitude. This is simply wishful thinking, they have no way of knowing whether they do or not – if they take their results at all seriously (and if they present their results to their peers then presumably this is the case) then they do have an obligation to try and ensure that the cause of their results is due to an intended rather than unintended interaction in their simulation.
There are a number of possible ways to try and prevent such a situation arising: including the independent replication of simulations on different systems, and the use of various kinds of representation (e.g. interval arithmetic) in simulations. However there is a more fundermental heuistic that may be applied: since the “artifact” presumably do not appear in reality (for this would simply indicate a deficiency of one’s mental model) then making one’s simulation more and more like reality will eventually get rid of the problem. For example, it is rare in natural (as opposed to constructed) systems that exact values have a critical and undesirable effect on outcomes because in that case the system would adapt (or evolve) to avoid this effect. Thus it is not generally plausible that humans determine their action upon crisp and critical comparisons (e.g. give money if their income is exactly greater than the average of their neighbours).
Limiting the language of representation
Perhaps the most far-reaching (and damaging) result of the use of numbers is that people become used to thinking of the phenomena in these numeric terms – what starts out as a working model or “proxy” for the phenomena ends up being mistaken for the truth about that phenomena. New students are trained to think in terms of the existing model and thus find it difficult to step back and rethink their way of thinking about a field. This effect is reinforced in some fields by “fashions” and traditions in modelling frameworks and styles – it can become necessary to utilise certain modelling forms or frameworks in order to get published or gain recognition.
For example, the usefullness of goods (or services) can be
represented as a total order amoung possible goods (and hence given a number
and compared as a utility).
However this does not mean that this is always a good model because
sometimes the nature of goods is critical to their usefulness. Whether one prefers A to B depends a great
deal on how these goods will be helpful and not how much they are helpful in the same way.
For example, with food flavourings it is the combination that makes it
preferable – there is no underlying utility of salt or sugar separate from the
contexts in which they are applied (say chips or strawberries)[1]. This is similar to the ranking of tennis
players: the ranking gives one a guess as to which of two players will win when
they play but does not determine this – the ranking is only a numerical model of who will win.
Before the advent
of cheap computational power it was very difficult to formally model without
using equations, because the manipulation of large amounts of data was very
difficult by hand. We no longer have
this excuse, we can now represent the qualitative processes directly, we do not
have to settle for equation-based models that require drastically reformulating
the problem to suit the technique (e.g. through the use of unrealistically
strong assumptions). The section below
has many examples where an early model of a fundermentally numeric nature
becomes part of an increasingly unjustifiable modelling tradition.
Some examples
In this section I consider some examples of numeric measures and consider how appropriate they are in an age of computational simulation modelling.
The Intelligent Quotient
The intelligence quotient (IQ) is a number assigned to people using a testing procedure that is supposed to indicate how intelligent they are compared to the population average. Essentially this is a score in a test that is scaled so that 100 is the average score etc. Most psychologists have long ago abandoned any thought that this number represents intelligence in general, retreating to the incredibly weak position that the only thing it really measures is success at the test itself (at least publically – there would be no point in continuing the test if they really thought so). More modern thinking approaches the problem in a more qualitative way: that there are many different kinds of intelligence (Gigerenzer ????). This, not only accords with everyday experience but has some support in terms of neurological evidence (CAT scans indicate that we sometimes use different parts of our brain for different kinds of tasks).
However the idea that there are some people that are “more” intelligent than others in some generic way still pervades the thinking of many people, including social simulators. Thus despite the fact that these different kinds of intelligence are more ameanable to formal modelling than a generic intelligence there are still social simulators that are applying the 1-dimensional numeric model of intelligence. For example …
Information
In 1949 Shannon formalised an aspect of information that was relevant to the capacity of communication channels in the form of a generalised entropy measure (Shannon and Weaver 1949). This was a probability-based measure concerning how different the communication was from a set of random signals. That this is nothing to do with what one usually identifies as “information” can be seen by the fact that it is possible to encode any message so that it is indistiguishable from a set of random signals (and thus has minimum Shannon information) regardless of how much information the message contains. Clearly in many circumstances it is not the extent to which a message reduces uncertainty but the way in which it reduces uncertainty. The impact of information is critically dependent upon the state of the receiving system – its usefulness comes out of the way the information relates to and changes that system. Despite this the Shannon model of information entropy is still used as a proxy for real communication in many models of social phenomena.
Opinion
Whilst it is quite legitmate to calculate the extent to which an opinion is held in a population and represent this as a real number, it is quite another to represent an opinion of an individual as such a number, even when it pertains to a single issue. In (Amblard et al. 2003) each state has an opinion interval which represents the range of its opinion about this issue, and a number which represents its uncertainty about the issue. Agents then influence each other depending on the overlap of their opinion intervals and their certainty. This “influence” mechanism is tried out on a variety of topologies and different sorts of convergence are observed in the results. They conclude by admiting that
The critique of these results in a sociological perspective is also a major challenge which is out of the scope of this paper.
In other words, there is no justification for the design of the model (there is none elsewhere in the paper). Despite this lack of justification for the model design they follow this with the claim that
… the idea of the necessity of a critical level of connectivity and some disorder in the network for extreme opinions to invade a population does not seem counterintuitive, and could find rich interpretation in real life sociological phenomena.
In other words that someone might be able to interpret this into sociological phenomena. Given that the labelling of the parts of this simulation in this paper are highly suggestive of an interpretation is in terms of the conditions under which “extremists” dominate opinion, this is simply unwise.
Dominance
In Hemelrijk’s paper (2003), a lot of the design and the results are closely related to the phenomena of concern: the dominance interactions of apes and their spatial distribution. However the “dominance” of an individual, the capacity of an individual to win a confrontation, is represented in terms of a single number. This number is increased if the individual wins its confrontations – it is an indication of where the individual is in the “dominance hierarchy” of the group. This assumes that (1) the dominance relation can be represented as a total order and (2) that an individual’s dominance changes according depending on the whether it wins confrontations in the way that is indicated. In a oral response to the above paper she said that sometimes intransistivities did occur but that this was rare. The implication is that there is a ranking amoung such small groups of apes and that all the members know this ranking. If this is the case, then using a numerical representation to encode the position of the apes in this ranking might be justified. However, that an individual’s change in position in the ranking can be determined by the equations seems more doubtful as the change in numerical value is dependent solely on the interaction of two apes (in a confrontation) whilst the position in the ranking depends on the values of all the apes in the troupe. This brings into doubt what the dominance value means.
Of course, if it can be demonstrated that either this does correspond well enough to what is observed with apes or that the rate of dominance increase on winning or loosing confrontations does not significantly effect the results then this method of representing dominance is adequate.
What are the viable alternatives?
Let me make it quite clear that I am not at all against formal or rigourous modelling. In fact, formal modelling is often essential for progress to be made (even if all the formal models are eventually discarded). However I am arguing that much of the modelling of social phenomena using numbers (or equations representing numeric relations) is, at best, unhelful and, at worst, counterproductively misleading.
A computational simulation is just as formal as an equation-based model. Each technique has its own advantages and limitations: equation-based modelling may allow for the declarative manipulation of the model to allow for closed-form solutions and other properties to be derived, however this is at the cost of the difficulty in relating the model to many phenomena; computational simulation can be more directly representational of the processes observed but is almost never ameanable to general solutions or formal manipulation. Thus although a computational simulation is a theory about some domain (if only a conceptual model) it retains much of the nature of an experiment. One can (almost) never know for sure about the nature of a simulation, but one can endlessly perform experiments upon it. We need to have models (either formal or otherwise) about what is happening in a simulation in order to be able to use it – each experiment which does not disconfirm our model of it leads us to have more confidence in the simulation. The greater the variety of experiments that the simulation survives (e.g. replication in another language) the more confidence we can have in its veracity. Using computational requires giving up an illusion that absolute proof or certainty is possible. This is frequently already the case even with analytic models because the equations are often analytically unsolvable so that either: approximations are required (which breaks the certainty of any proof) or numerical simulations are required (in which case one has no more certainty than any other simulation). There is no practical difference between: a huge system of equations which has a set of equations to describe the state of each agent sperately and another set to describe all the relations between each agent that interacts; and a distributed computational simulation that encodes the same things – one has the same practical options in each case.
One practical way forward is to formulate and maintain “chains” (or even as Giere (1988) puts it “clusters) of models at different levels of abstraction, starting from the bottom up. Thus the first step is to decide what “data models” of the target phenomena are appropriate (including ancedotal accounts and qualitative observations). Then a “descriptive” simulation can be developed – this is intended to include as much of the relevant detail and processes as possible in as direct a manner as possible. This is akin to a natural language description, except that it makes the first steps towards abstraction – a simulation is appropriate because it enables processes to be captured as well as states. Such a descriptive simulation has several purposes: it is a tool to inform (and be informed by) observation by helping frame what are the important questions to investigate; it allows for the exploration of the behaviour in a detailed and flexible manner enabling the complex processes to be understood; it opens up the description to critism by experts and stakeholders so that the model can be more easily improved; and it stages the abstraction providing a better basis for more abstract models to be tested and formulated.
Thus a simulation can be used to stage the abstraction process. The relationship between the simulation and the observations of the phenomena is relatively transparent and direct. The more abstract models can intended to capture aspects of the behaviour can be informed by and tested against runs of the descriptive simulation. This has some great advantages over the direct modelling of phenomena with abstract models: one can use the simulation to establish whether and under what conditions the more abstract models work (which should correspond with when their assumptions hold); and the simulation gives justification for the details of the abstract model so that when one is asked why the model is formulated as it is one can point to the simulation runs that it models. The simulation delays the abstraction by providing an experimental test-bed which is as rich a representation of the phenomena as possible. This staging of the abstraction is illustrated in Figure 1 below.
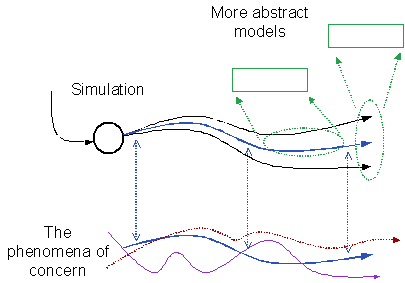
Figure 1. Using a simulation stage abstraction
The more abstract model could be an equation-based model or a more abstract computational simulation. In this manner one can build up a whole hierarchy of models of different levels of abstraction (as in Figure 2 below).
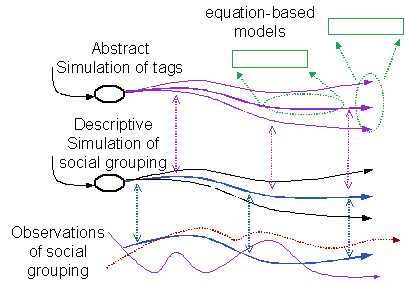
Figure
2. A chain
of three levels of model with increasing abstraction concerning tag-based
mechanisms of group formation
This combination of computational simulation and the a posteriori formulation of abstract models seems to hold out the hope for the achievmenbt of the best combination of advantages possible for complex phenomena, albeit at the cost of a lot more work.
Conclusion
The advent of cheap and available computational power has deprived us of any excuse for the innappropriate use of numeric representation. Many of the examples of this sort of approach is merely a “hang-over” from the time before this was the case. This shifts the burdon of proof upon those onto those who claim to be investigating “abstract social properties” using such naïve representations to show that what they are are doing is in fact likely to be relevant to actually occuring social phenomena and so that it does not critcally distort the phenomena. Until there is some evidence that this might actually be the case there is little reason to give any attention to their results.
Surely the fact that the model design and its results seem plausible to the authors is insufficient justification? During the 1930’s there flourished a “science” of phrenology which studied how personality types could be predicted from the shape of the skull. This was highly plausible, especially to the academics involved. However it turned out to be a total red-herring – there was never any credible independent evidence or justification to support their contentions.
Acknowledgements
I would like to thank the authors of the papers at the 1st ESSA conference for the opportunity and motivation to write this paper. As always, ideas closely related to this have been extensively discussed with Scott Moss and David Hales. I feel I also should acknowledge my PhD examiners (albeit relactantly) for making me rewrite my thesis using measure theory – who knows how I would have otherwise wasted the time that that took?
References
Edmonds, B. (2000) The Purpose and Place of Formal Systems in the Development of Science, CPM Report 00-75, MMU, UK. (http://cfpm.org/cpmrep75.html)
Edmonds, B. (2002) Simplicity is Not Truth-Indicative. CPM Report 02-00, MMU, 2002 (http://cfpm.org/cpmrep99.html).
Edmonds, B. (2003). Towards an ideal social simulation language. In Sichman, J. et al (eds.), Multi-Agent-Based Simulation II: 3rd Int. Workshop, (MABS02), Revised Papers, pages 104-124, Springer, LNAI, 2581.
Edmonds, B. and Hales, D. (2003a) Computational Simulation as Theoretical Experiment, CPM report 03-106, MMU, 2003 (http://cfpm.org/cpmrep106.html).
Edmonds, B. and Hales, D. (2003b) Replication, Replication and Replication - Some Hard Lessons from Model Alignment. Journal of Artificial Societies and Social Simulation 6(4) (http://jasss.soc.surrey.ac.uk/6/4/11.html)
Amblard, F. Weisbuch, G. and Deffuant, G. (2003), The drift to a single extreme appears only beyond a critical connectivity of the social networks - Study of the relative agreement opinion dynamics on small world networks. 1st International Conference of the European Society for Social Simulation (ESSA 2003), Groningen, September 2003.
Giere R., N. (1988). Explaining science : a cognitive approach. Chicago ; London, University of Chicago Press.
Gigerenzer, G. and D. G. Goldstein (1996). "Reasoning the fast and frugal way: Models of bounded rationality." Psychological Review 104: 650-669.
Gödel, K. (1930) Die Vollständigkeit der Axiome des logischen Funktionen-kalküls, Monatshefte für Mathematik und Physik 37, 349-360.
Hemelrijk, C. K. (2003) Social phenomena emerging by self-organisation in a competitive, virtual world (‘DomWorld’). 1st International Conference of the European Society for Social Simulation (ESSA 2003), Groningen, September 2003.
Krantz, D. H., Luce, R. D., Suppes, P., and Tversky, A. (1971). Foundations of measurement. (Vol. I: Additive and polynomial representations.). New York: Academic Press.
Luce, R. D., Krantz, D. H., Suppes, P., and Tversky, A. (1990). Foundations of measurement. (Vol. III: Representation, axiomatization, and invariance). New York: Academic Press.
Polhill, J. G. Luis R. Izquierdo, & Nicholas M. Gotts - The Ghost in the Model (and other effects of floating point arithmetic) 1st International Conference of the European Society for Social Simulation (ESSA 2003), Groningen, September 2003.
Riolo, R. L., Cohen, M. D. and Axelrod, R (2001), Evolution of cooperation without reciprocity. Nature, 411:441-443.
Sarle, W. S. (1997) Measurement theory: Frequently asked questions, Version 3, Sep 14, 1997. (Accessed 22/01/04) ftp://ftp.sas.com/pub/neural/measurement.html
Shannon, C. E. and W. Weaver (1949). The Mathematical Theory of Communication. Urbana, Illinois, University of Illinois Press.
Stevens, S. S. (1946), On the theory of scales of measurement. Science, 103:677-680.
Suppes, P., Krantz, D. H., Luce, R. D., and Tversky, A. (1989). Foundations of measurement. (Vol. II: Geometrical, threshold, and probabilistic respresentations). New York: Academic Press.
Whitehead, A. N. and Russell, B. (1962) Principia mathematica. Cambridge: Cambridge University Press (originally published 1913).